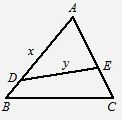题目内容
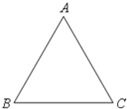 在边长为1的等边三角形ABC中,设
在边长为1的等边三角形ABC中,设| BC |
| a |
| CA |
| b |
| AB |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
A、
| ||
B、-
| ||
| C、0 | ||
| D、3 |
分析:根据三角形是边长为1的正三角形,看出要求数量积的两个向量之间的夹角,利用数量积的公式写出结果.
解答:解:∵三角形是边长为1的正三角形,
∴
•
+
•
+
•
=1×1×(-
)+1×1×(-
)+1×1×(-
)
=-
故选B.
∴
| a |
| b |
| b |
| c |
| c |
| a |
=1×1×(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 3 |
| 2 |
故选B.
点评:本题考查向量的数量积,本题解题的关键是看清两个向量的夹角,三角形的内角不是两个向量的夹角,而是内角的补角是两个向量的夹角.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 形状的三角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
形状的三角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.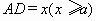 ,
,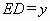 ,求用
,求用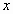 表示
表示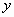 的函数关系式.
的函数关系式.