题目内容
 (2006•黄浦区二模)设a为正数,直角坐标平面内的点集A={(x,y)|x,y,a-x-y是三角形的三边长}.
(2006•黄浦区二模)设a为正数,直角坐标平面内的点集A={(x,y)|x,y,a-x-y是三角形的三边长}.(1)画出A所表示的平面区域;
(2)在平面直角坐标系中,规定a∈Z,且y∈Z时,(x,y)称为格点,当a=8时,A内有几个格点(本小题只要直接写出结果即可);
(3)点集A连同它的边界构成的区域记为
. |
| A |
. |
| A |
分析:(1)根据三角形的三边满足的条件2x+2y>a; a>2y;a>2x,画出A所表示的平面区域;
(2)当a=8时,结合图形列出A内的格点,得到格点个数,
(3)结合图象,当圆与三角形相切时半径最大,根据等面积法求出r的最大值.
(2)当a=8时,结合图形列出A内的格点,得到格点个数,
(3)结合图象,当圆与三角形相切时半径最大,根据等面积法求出r的最大值.
解答:解:(1)集合A表示一个点集(平面上一组点),这些点的横纵坐标满足:2x+2y>a; a>2y;a>2x
其中a是正数.
表示一个由直线2x+2y=a 和x=
和y=
围成的三角形区域.
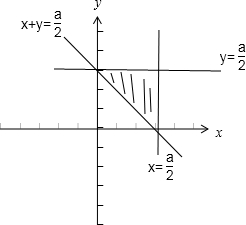
(2)当a=8时,A内的格点有(2,3),(3,2),(3,3)共3个格点.
(3)结合图象,当圆与三角形相切时半径最大,根据等面积法得到
r+
r+
ar=
×
解得r=
a
其中a是正数.
表示一个由直线2x+2y=a 和x=
| a |
| 2 |
| a |
| 2 |

(2)当a=8时,A内的格点有(2,3),(3,2),(3,3)共3个格点.
(3)结合图象,当圆与三角形相切时半径最大,根据等面积法得到
| a |
| 2 |
| a |
| 2 |
| ||
| 2 |
| a |
| 2 |
| a |
| 2 |
解得r=
2-
| ||
| 4 |
点评:本题考查画不等式组表示的平面区域是解决线性规划问题的关键,当圆与三角形相切时三角形内的圆半径最大,属于中档题.

练习册系列答案
相关题目