题目内容
已知函数f(x)=2sin(ωx+ ),x∈R,其中ω>0,-π<
),x∈R,其中ω>0,-π< ≤π.若f(x)的最小正周期为6π,且当x=
≤π.若f(x)的最小正周期为6π,且当x= 时,f(x)取得最大值,则( )
时,f(x)取得最大值,则( )
(A)f(x)在区间[-2π,0]上是增函数
(B)f(x)在区间[-3π,-π]上是增函数
(C)f(x)在区间[3π,5π]上是减函数
(D)f(x)在区间[4π,6π]上是减函数
【答案】
A
【解析】∵T=6π,
∴ω=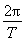 =
=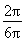 =
=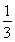 ,
,
∴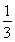 ×
×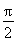 +
+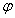 =2kπ+
=2kπ+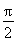 (k∈Z),
(k∈Z),
∴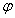 =2kπ+
=2kπ+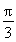 (k∈Z).
(k∈Z).
∵-π<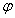 ≤π,
≤π,
∴令k=0得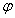 =
=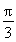 .
.
∴f(x)=2sin(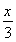 +
+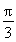 ).
).
∴增区间为2kπ-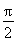 <
<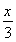 +
+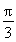 <2kπ+
<2kπ+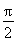 ,k∈Z,
,k∈Z,
∴2kπ-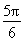 <
<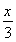 <2kπ+
<2kπ+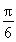 ,k∈Z,
,k∈Z,
∴6kπ-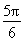 <x<6kπ+
<x<6kπ+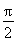 ,k∈Z,
,k∈Z,
当k=0时,-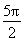 <x<
<x<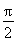 .
.
∴f(x)在[-2π,0]上是增函数.故选A.

练习册系列答案
相关题目