题目内容
设关于x的函数f(x)=-cos2x-2msinx+m2+2m的最小值是m的函数,记为g(m).(1)求g(m)的解析表达式;
(2)当g(m)=5时,求m的值;
(3)如果方程f(x)=0在x∈(0,π)有两不相等的解,求实数m的取值范围.
【答案】分析:(1)先对f(x)进行变形:f(x)=sin2x-2msinx+m2+2m-1,令t=sinx,则t∈[-1,1],函数可变为h(t)=t2-2mt+m2+2m-1=(t-m)2+2m-1,按对称轴与区间[-1,1]的位置分三种情况讨论即可求得g(0);
(2)由(1)分三种情况解g(m)=5即可;
(3)方程f(x)=0在x∈(0,π)有两不相等的解,等价于h(t)=t2-2mt+m2+2m-1=0在t∈(0,1)上有一解,问题转化为函数h(t)(0,1)上有一个零点,由此即可得到关于m的限制条件;
解答:解:(1)f(x)=sin2x-2msinx+m2+2m-1,
令t=sinx,则t∈[-1,1],
则函数可变为h(t)=t2-2mt+m2+2m-1=(t-m)2+2m-1,
图象开口向上,对称轴为t=m,
①当m<-1时,g(m)=h(-1)=m2+4m;
②当-1≤m≤1时,g(m)=h(m)=2m-1;
③当m>1时,g(m)=h(1)=m2.
所以g(m)=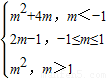 .
.
(2)当g(m)=5时,
若m<-1,有m2+4m=5,解得m=-5或m=1(舍);
若-1≤m≤1,有2m-1=5,解得m=3(舍);
若m>1,有m2=5,解得m=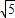 或-
或-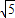 (舍);
(舍);
综上知,m=-5或m=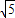 .
.
(3)方程f(x)=0在x∈(0,π)有两不相等的解,由(1)知:等价于h(t)=t2-2mt+m2+2m-1=0在t∈(0,1)上有一解,
则 或h(0)•h(1)<0,即m=
或h(0)•h(1)<0,即m= 或(m2+2m-1)m2<0,所以m=
或(m2+2m-1)m2<0,所以m= 或-1-
或-1-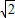 <m<-1+
<m<-1+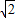 ,且m≠0,
,且m≠0,
所以m的取值范围为:m= 或m∈(-1-
或m∈(-1-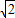 ,0)∪(0,-1+
,0)∪(0,-1+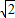 ).
).
点评:本题考查二次函数在闭区间上的最值问题、分段函数求值及函数的零点,属中档题,本题具有一定综合性,需要掌握相关基础知识.
(2)由(1)分三种情况解g(m)=5即可;
(3)方程f(x)=0在x∈(0,π)有两不相等的解,等价于h(t)=t2-2mt+m2+2m-1=0在t∈(0,1)上有一解,问题转化为函数h(t)(0,1)上有一个零点,由此即可得到关于m的限制条件;
解答:解:(1)f(x)=sin2x-2msinx+m2+2m-1,
令t=sinx,则t∈[-1,1],
则函数可变为h(t)=t2-2mt+m2+2m-1=(t-m)2+2m-1,
图象开口向上,对称轴为t=m,
①当m<-1时,g(m)=h(-1)=m2+4m;
②当-1≤m≤1时,g(m)=h(m)=2m-1;
③当m>1时,g(m)=h(1)=m2.
所以g(m)=
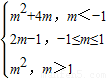 .
.(2)当g(m)=5时,
若m<-1,有m2+4m=5,解得m=-5或m=1(舍);
若-1≤m≤1,有2m-1=5,解得m=3(舍);
若m>1,有m2=5,解得m=
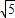 或-
或-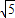 (舍);
(舍);综上知,m=-5或m=
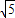 .
.(3)方程f(x)=0在x∈(0,π)有两不相等的解,由(1)知:等价于h(t)=t2-2mt+m2+2m-1=0在t∈(0,1)上有一解,
则
 或h(0)•h(1)<0,即m=
或h(0)•h(1)<0,即m= 或(m2+2m-1)m2<0,所以m=
或(m2+2m-1)m2<0,所以m= 或-1-
或-1-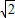 <m<-1+
<m<-1+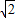 ,且m≠0,
,且m≠0,所以m的取值范围为:m=
 或m∈(-1-
或m∈(-1-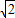 ,0)∪(0,-1+
,0)∪(0,-1+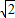 ).
).点评:本题考查二次函数在闭区间上的最值问题、分段函数求值及函数的零点,属中档题,本题具有一定综合性,需要掌握相关基础知识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,其中p≤0,若对任意的x∈[1,2],总有2f(x)≥g(x)+4x-2x2成立,求p的取值范围.
,其中p≤0,若对任意的x∈[1,2],总有2f(x)≥g(x)+4x-2x2成立,求p的取值范围. ,其中p≤0,若对任意的x∈[1,2],总有2f(x)≥g(x)+4x-2x2成立,求p的取值范围.
,其中p≤0,若对任意的x∈[1,2],总有2f(x)≥g(x)+4x-2x2成立,求p的取值范围. ,若对任意的x∈[1,2],2f(x)≥g(x)+4x﹣2x2恒成立,求实数p的取值范围.
,若对任意的x∈[1,2],2f(x)≥g(x)+4x﹣2x2恒成立,求实数p的取值范围.  ,若对任意的x∈[1,2],2f(x)≥g(x)+4x-2x2恒成立,求实数p的取值范围.
,若对任意的x∈[1,2],2f(x)≥g(x)+4x-2x2恒成立,求实数p的取值范围. ,若对任意的x∈[1,2],2f(x)≥g(x)+4x-2x2恒成立,求实数p的取值范围.
,若对任意的x∈[1,2],2f(x)≥g(x)+4x-2x2恒成立,求实数p的取值范围.