题目内容
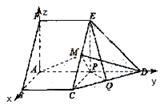
()如图,在五面体ABCDEF中,FA ![]() 平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB![]() AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=![]() AD
AD
(I) 求异面直线BF与DE所成的角的大小;
(II) 证明平面AMD![]() 平面CDE;
平面CDE;
(III)求二面角A-CD-E的余弦值。
⑴60°,⑵略,⑶![]()
解析:
本小题要考查异面直线所成的角、平面与平面垂直、二面角等基础知识,考查用空间向量解决立体几何问题的方法,考查空间想像能力、运算能力和推理论证能力。满分12分.
方法一:(Ⅰ)由题设知,BF//CE,所以∠CED(或其补角)为异面直线BF与DE所成的角。设P为AD的中点,连结EP,PC。因为FE![]() AP,所以FA
AP,所以FA![]() EP,同理AB
EP,同理AB![]() PC。又FA⊥平面ABCD,所以EP⊥平面ABCD。而PC,AD都在平面ABCD内,故EP⊥PC,EP⊥AD。由AB⊥AD,可得PC⊥AD设FA=a,则EP=PC=PD=a,CD=DE=EC=
PC。又FA⊥平面ABCD,所以EP⊥平面ABCD。而PC,AD都在平面ABCD内,故EP⊥PC,EP⊥AD。由AB⊥AD,可得PC⊥AD设FA=a,则EP=PC=PD=a,CD=DE=EC=![]() ,故∠CED=60°。所以异面直线BF与DE所成的角的大小为60°
,故∠CED=60°。所以异面直线BF与DE所成的角的大小为60°
(II)证明:因为![]()
![]()
(III)![]()
![]()
由(I)可得,![]()
![]()
方法二:如图所示,建立空间直角坐标系,
点![]() 为坐标原点。设
为坐标原点。设![]() 依题意得
依题意得![]()
![]()
![]()
![]()
![]()
![]()
(I)![]()
![]()
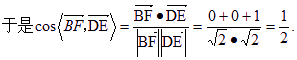
所以异面直线![]() 与
与![]() 所成的角的大小为
所成的角的大小为![]() .
.
(II)证明:![]()
![]()
![]() ,
,
![]()
![]()
(III)
![]()
![]()
又由题设,平面![]() 的一个法向量为
的一个法向量为![]()
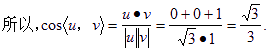

练习册系列答案
相关题目
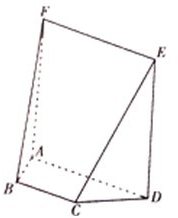 如图,在五面体EF-ABCD中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=l,AD=2
如图,在五面体EF-ABCD中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=l,AD=2 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,△ABF、△CDE是等边三角形,CD=1,EF=
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,△ABF、△CDE是等边三角形,CD=1,EF=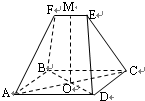 如图,在五面体ABCDEF中,四边形ABCD为矩形,对角线AC,BD的交点为O,△ABF和△DEC为等边三角形,棱EF∥BC,EF=
如图,在五面体ABCDEF中,四边形ABCD为矩形,对角线AC,BD的交点为O,△ABF和△DEC为等边三角形,棱EF∥BC,EF=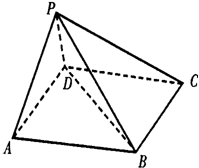 如图,在五面体P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,PB=
如图,在五面体P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,PB= (2013•广元二模)如图,在五面体EF-ABCD中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=l,AD=2
(2013•广元二模)如图,在五面体EF-ABCD中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=l,AD=2