题目内容
直线 恒过定点
恒过定点 ,且点
,且点 在直线
在直线 (
( )上,则
)上,则 的最小值为
的最小值为
A. | B. | C. | D. |
B
解析试题分析:先求出定点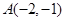 ,再将
,再将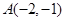 代入直线
代入直线 ,得到关于m、n的关系式,由基本不等式得:
,得到关于m、n的关系式,由基本不等式得: =
=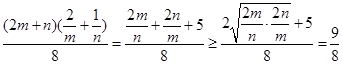
解:直线 恒过定点
恒过定点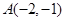 ,把A代入直线
,把A代入直线 得:
得: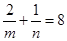 ,所以
,所以 =
= ,则
,则 的最小值为
的最小值为 。故选B。
。故选B。
考点:基本不等式.
点评:本题主要考查直线过定点问题和基本不等式的运用.考查基础知识的综合运用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
下列不等式正确的是
A.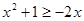 | B.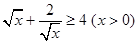 |
C.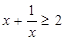 | D.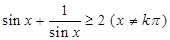 |
下列结论正确的是( )
A.当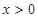 且 且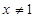 时, 时,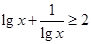 ; ; | B.当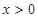 时, 时,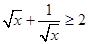 ; ; |
C.当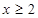 时, 时,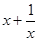 的最小值为2; 的最小值为2; | D.当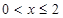 时, 时,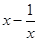 无最大值; 无最大值; |
设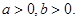 若
若 的最小值为( )
的最小值为( )
| A.8 | B.4 | C.1 | D.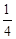 |
设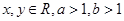 ,若
,若 ,则
,则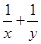 的最大值为( )
的最大值为( )
| A.2 | B.3 | C.4 | D.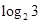 |
已知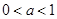 ,
,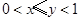 ,且
,且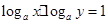 ,那么
,那么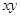 的取值范围是( )
的取值范围是( )
A.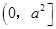 | B.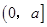 | C.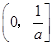 | D.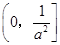 |
设 的最小值是( )
的最小值是( )
| A.10( | B. | C. | D. |
如果 ,那么
,那么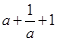 的最小值是( )
的最小值是( )
| A.2 | B.3 | C.4 | D.5 |
设正实数 满足
满足 ,则当
,则当 取得最大值时,
取得最大值时, 的最大值为( )
的最大值为( )
A. | B. | C. | D. |