题目内容
A.若关于x的不等式|x+1|+|x-3|≥a恒成立,则实数a的取值范围是 .B.如图,AB是⊙O的直径,P是AB延长线上的一点,过P作⊙O的切线,切点为C,PC=2
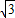 ,若∠CAP=30°,则⊙O的直径AB= .
,若∠CAP=30°,则⊙O的直径AB= .C.已知直线的极坐标方程为ρsin(θ+
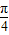 )=
)=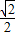 ,则极点到这条直线的距离是 .
,则极点到这条直线的距离是 .
【答案】分析:A.利用不等式|x+m|+|x+n|≥|m-n|即可求出a的取值范围;
B.连接OC,利用切线的性质及直接三角形中的边角关系即可求出半径OC;
C.先将直线的极坐标方程化为普通方程,再利用点到直线的距离公式即可.
解答:解:A.∵关于x的不等式|x+1|+|x-3|≥a恒成立?(|x+1|+|x-3|)min≥a,而|x+1|+|x-3|≥|x+1-(x-3)|=4,∴实数a的取值范围是a≤4,
故答案为a≤4;
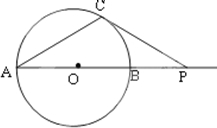
B.由题意作出图形:
 连接OC,∵PC是圆O的切线,∴OC⊥PC,∠OCP=90°.
连接OC,∵PC是圆O的切线,∴OC⊥PC,∠OCP=90°.
∵∠CAO=30°,OC=OA,∴∠COP=60°,∴∠CPO=30°.
在Rt△OCP中,OC=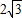 tan30°=2;∴直径AB=4,
tan30°=2;∴直径AB=4,
故答案为4;
C.∵直线的极坐标方程为ρsin(θ+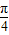 )=
)=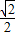 ,则展开为
,则展开为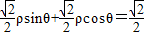 ,化为普通方程x+y-1=0,
,化为普通方程x+y-1=0,
则极点即原点到这条直线的距离d=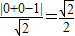 ,
,
故答案为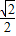 .
.
点评:正确理解不等式|x+m|+|x+n|≥|m-n|、切线的性质、点到直线的距离公式是解题的关键.
B.连接OC,利用切线的性质及直接三角形中的边角关系即可求出半径OC;
C.先将直线的极坐标方程化为普通方程,再利用点到直线的距离公式即可.
解答:解:A.∵关于x的不等式|x+1|+|x-3|≥a恒成立?(|x+1|+|x-3|)min≥a,而|x+1|+|x-3|≥|x+1-(x-3)|=4,∴实数a的取值范围是a≤4,
故答案为a≤4;
B.由题意作出图形:
 连接OC,∵PC是圆O的切线,∴OC⊥PC,∠OCP=90°.
连接OC,∵PC是圆O的切线,∴OC⊥PC,∠OCP=90°.∵∠CAO=30°,OC=OA,∴∠COP=60°,∴∠CPO=30°.
在Rt△OCP中,OC=
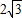 tan30°=2;∴直径AB=4,
tan30°=2;∴直径AB=4,故答案为4;
C.∵直线的极坐标方程为ρsin(θ+
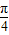 )=
)=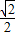 ,则展开为
,则展开为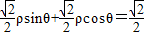 ,化为普通方程x+y-1=0,
,化为普通方程x+y-1=0,则极点即原点到这条直线的距离d=
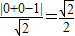 ,
,故答案为
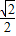 .
.点评:正确理解不等式|x+m|+|x+n|≥|m-n|、切线的性质、点到直线的距离公式是解题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
0<b<1+a,若关于x的不等式(x-b)2>(ax)2的解集中的整数恰有3个,则( )
| A、-1<a<0 | B、0<a<1 | C、1<a<3 | D、2<a<3 |
 A.若关于x的不等式|x+1|+|x-3|≥a恒成立,则实数a的取值范围是
A.若关于x的不等式|x+1|+|x-3|≥a恒成立,则实数a的取值范围是