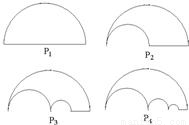
题目内容
如图P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为
的半圆后得到图形P2,然后依次剪去一个更小半圆(其直径为前一个被剪掉半圆的半径)得圆形P3,P4,…,Pn,…,记纸板Pn的面积为Sn,则Sn=
[1-
]
[1-
].
| 1 |
| 2 |
| π |
| 2 |
1-(
| ||
| 3 |
| π |
| 2 |
1-(
| ||
| 3 |

分析:由已知每次剪掉的半圆形面积构成一个等比数列,根据已知不难求出该数列的首项和公比,代入等比数列前n项和公式,易得剪去的所有半圆的面积和,从而得到最后纸板Pn的面积.
解答:解:每次剪掉的半圆形面积构成一个以
为首项,以
为公比的等比数列,
∴纸板Pn的面积为Sn=
-
=
[1-
].
故答案为:
[1-
].
| π |
| 8 |
| 1 |
| 4 |
∴纸板Pn的面积为Sn=
| π |
| 2 |
| ||||
1-
|
| π |
| 2 |
1-(
| ||
| 3 |
故答案为:
| π |
| 2 |
1-(
| ||
| 3 |
点评:本题考查等比数列在生产实际中的应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
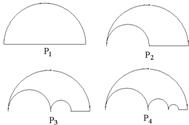 如图P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为
如图P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为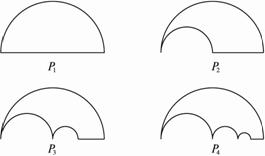
 的半圆后得到图形P2,然后依次剪去一个更小半圆(其直径为前一个被剪掉半圆的半径)得圆形P3、P4、…..Pn…,记纸板Pn的面积为Sn,则
的半圆后得到图形P2,然后依次剪去一个更小半圆(其直径为前一个被剪掉半圆的半径)得圆形P3、P4、…..Pn…,记纸板Pn的面积为Sn,则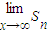 = .
= .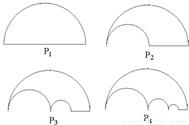
 的半圆后得到图形P2,然后依次剪去一个更小半圆(其直径为前一个被剪掉半圆的半径)得圆形P3、P4、…..Pn…,记纸板Pn的面积为Sn,则
的半圆后得到图形P2,然后依次剪去一个更小半圆(其直径为前一个被剪掉半圆的半径)得圆形P3、P4、…..Pn…,记纸板Pn的面积为Sn,则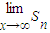 = .
= .