题目内容
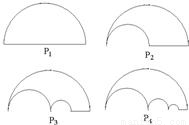
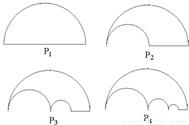
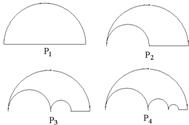 如图P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为
如图P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为| 1 |
| 2 |
| lim |
| n→∞ |
分析:由已知每次剪掉的半圆形面积构成一个等比数列,根据已知不难求出该数列的首项和公比,代入等比数列前n项和公式,易得剪去的所有半圆的面积和,从而得到最后纸板Pn的面积.
解答:解:每次剪掉的半圆形面积构成一个以
为首项,以
为公比的等比数列,
则
a1+a2+…+an=
=
故:
Sn=
-
=
故答案为:
| π |
| 8 |
| 1 |
| 4 |
则
| lim |
| n→∞ |
| ||
1-
|
| π |
| 6 |
故:
| lim |
| n→∞ |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
故答案为:
| π |
| 3 |
点评:本题考查的知识点其实是一种极限思想,当一个等比数列的|q|<1时,
qn=0,则
a1+a2+…+an=
.
| lim |
| n→∞ |
| lim |
| n→∞ |
| a1 |
| 1-q |

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目

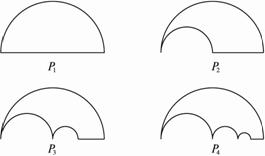
 的半圆后得到图形P2,然后依次剪去一个更小半圆(其直径为前一个被剪掉半圆的半径)得圆形P3、P4、…..Pn…,记纸板Pn的面积为Sn,则
的半圆后得到图形P2,然后依次剪去一个更小半圆(其直径为前一个被剪掉半圆的半径)得圆形P3、P4、…..Pn…,记纸板Pn的面积为Sn,则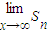 = .
= .
 的半圆后得到图形P2,然后依次剪去一个更小半圆(其直径为前一个被剪掉半圆的半径)得圆形P3、P4、…..Pn…,记纸板Pn的面积为Sn,则
的半圆后得到图形P2,然后依次剪去一个更小半圆(其直径为前一个被剪掉半圆的半径)得圆形P3、P4、…..Pn…,记纸板Pn的面积为Sn,则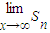 = .
= .