题目内容
一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在一个球面上,则这个球的表面积是( )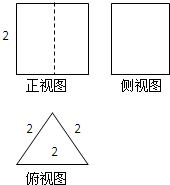

分析:由三视图知,几何体是一个三棱柱,三棱柱的底面是边长为2的正三角形,侧棱长是2,根据三棱柱的两个底面的中心的中点与三棱柱的顶点的连线就是外接球的半径,求出半径即可求出球的表面积.
解答:解:由三视图知,几何体是一个三棱柱,三棱柱的底面是边长为2的正三角形,侧棱长是2,
三棱柱的两个底面的中心的中点与三棱柱的顶点的连线就是外接球的半径,
r=
=
,球的表面积4πr2=
π.
故选C.
三棱柱的两个底面的中心的中点与三棱柱的顶点的连线就是外接球的半径,
r=
(
|
|
| 28 |
| 3 |
故选C.
点评:本题是中档题,考查三棱柱的外接球的表面积的求法,外接球的半径是解题的关键,考查计算能力.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
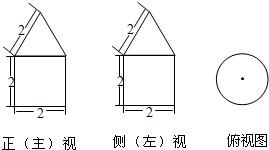 一个空间几何体的三视图如图所示,则该几何体的体积为( )
一个空间几何体的三视图如图所示,则该几何体的体积为( )A、2π+
| ||||
B、
| ||||
C、2π+
| ||||
D、4π+
|
一个空间几何体的三视图如图所示,则该几何体的表面积为( )
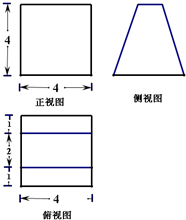

| A、48 | ||
B、32+8
| ||
C、48+8
| ||
| D、80 |
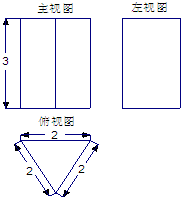 已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的表面积是
已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的表面积是 已知一个空间几何体的三视图如图所示,主视图、侧视图是斜边长为
已知一个空间几何体的三视图如图所示,主视图、侧视图是斜边长为 已知一个空间几何体的三视图如图所示,则这个几何体的表面积是
已知一个空间几何体的三视图如图所示,则这个几何体的表面积是