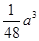题目内容
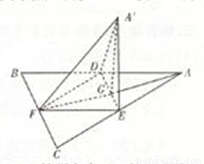
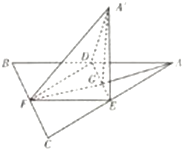 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,将△ADE绕DE旋转得到△A′DE(A′∉平面ABC),则下列叙述错误的是( )
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,将△ADE绕DE旋转得到△A′DE(A′∉平面ABC),则下列叙述错误的是( )分析:由线线垂直⇒线面垂直⇒面面垂直,可判断A正确;
由线面平行的判定定理,可判断B正确;
由棱锥的体积公式,可判断当高最大时,体积最大,求出体积的最大值,可判断C错误;
由异面直线的判定定理可判断D正确.
由线面平行的判定定理,可判断B正确;
由棱锥的体积公式,可判断当高最大时,体积最大,求出体积的最大值,可判断C错误;
由异面直线的判定定理可判断D正确.
解答:解:∵△ABC是正三角形,∴A'G⊥DE,DE⊥FG,∴DE⊥平面A′FG,DE?平面ABC,∴平面A′FG⊥平面ABC,故A正确
∵BC∥DE,BC?平面A′DE,DE?平面A′DE,∴BC∥平面A′DE,故B正确
当A′G⊥平面ABC时,三棱锥A′-DEF的高为A′G,而底面DEF的面积一定,
∴三棱锥A′-DEF的体积最大值为
×
×
×
a×
a=
a3,故C错误;
∵A′∉平面ABC,由异面直线的判定定理,直线DF与直线A′E是异面直线,故D正确.
故选C.
∵BC∥DE,BC?平面A′DE,DE?平面A′DE,∴BC∥平面A′DE,故B正确
当A′G⊥平面ABC时,三棱锥A′-DEF的高为A′G,而底面DEF的面积一定,
∴三棱锥A′-DEF的体积最大值为
| 1 |
| 3 |
| 1 |
| 2 |
| a |
| 2 |
| ||
| 2×2 |
| ||
| 4 |
| 1 |
| 64 |
∵A′∉平面ABC,由异面直线的判定定理,直线DF与直线A′E是异面直线,故D正确.
故选C.
点评:本题以折叠图形为载体,考查面面垂直的判定,线面平行的判定,棱锥的体积公式及异面直线的判定,解题的关键是利用好折叠前的位置关系.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
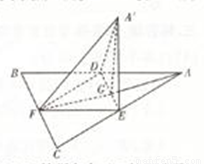
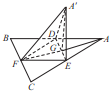 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题: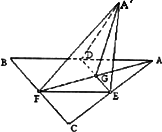
 平面ABC),则下列叙述错误的是(
)
平面ABC),则下列叙述错误的是(
)
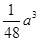
 平面ABC),则下列叙述错误的是(
)
平面ABC),则下列叙述错误的是(
)