题目内容
(本题满分12分)
已知函数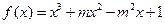 (m为常数,且m>0)有极大值9.
(m为常数,且m>0)有极大值9.
(1)求m的值;
(2)若斜率为-5的直线是曲线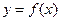 的切线,求此直线方程.
的切线,求此直线方程.
已知函数
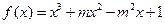 (m为常数,且m>0)有极大值9.
(m为常数,且m>0)有极大值9.(1)求m的值;
(2)若斜率为-5的直线是曲线
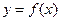 的切线,求此直线方程.
的切线,求此直线方程.解:(Ⅰ) f’(x)=3x2+2mx-m2=(x+m)(3x-m)=0,则x=-m或x= m,
m,
当x变化时,f’(x)与f(x)的变化情况如下表:
从而可知,当x=-m时,函数f(x)取得极大值9,
即f(-m)=-m3+m3+m3+1=9,∴m=2.
(Ⅱ)由(Ⅰ)知,f(x)=x3+2x2-4x+1,
依题意知f’(x)=3x2+4x-4=-5,∴x=-1或x=- .
.
又f(-1)=6,f (- )=
)= ,
,
所以切线方程为y-6=-5(x+1),或y- =-5(x+
=-5(x+ ),
),
即5x+y-1=0,或135x+27y-23=0.
 m,
m,当x变化时,f’(x)与f(x)的变化情况如下表:
| x | (-∞,-m) | -m | (-m,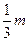 ) ) | 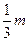 | (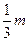 ,+∞) ,+∞) |
| f’(x) |  + + | 0 | - | 0 | + |
| f (x) | | 极大值 | | 极小值 | |
即f(-m)=-m3+m3+m3+1=9,∴m=2.
(Ⅱ)由(Ⅰ)知,f(x)=x3+2x2-4x+1,
依题意知f’(x)=3x2+4x-4=-5,∴x=-1或x=-
 .
.又f(-1)=6,f (-
 )=
)= ,
,所以切线方程为y-6=-5(x+1),或y-
 =-5(x+
=-5(x+ ),
),即5x+y-1=0,或135x+27y-23=0.
略

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 的定义域为( )
的定义域为( ) B.
B. C.
C. D.
D.
 且
且 。
。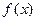 的解析式及定义域。(Ⅱ)求
的解析式及定义域。(Ⅱ)求
 数
数 的定义域;
的定义域; 的定义域为_________.
的定义域为_________.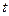 是负实数,则函数
是负实数,则函数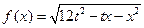 的定义域是
的定义域是