题目内容
正四棱柱ABCD-A1B1C1D1中,已知AB=2,E、F分别是D1B、AD的中点,![]() .
.
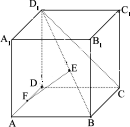
(1)建立适当的坐标系,求点E的坐标;
(2)证明:EF⊥面D1BC;
(3)求二面角D1-BF-C的余弦值.
答案:
解析:
解析:
|
(1)如图建立空间直角坐标系,设DD1=a,则D(0,0,0),D1(0,0,a),C(0,2,0),B(2,2,0) (2)由(1)知: 又 又D1B (3)由D向BF的延长线作垂线,垂足为M,连结D1M,则D1M 则 在 |

练习册系列答案
相关题目
已知正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为AA1中点,则异面直线BE与CD1所成角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
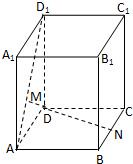 如图,在正四棱柱ABCD-A1B1C1D1中,AA1=2,AB=1,M、N分别在AD1,BC上移动,并始终保持MN∥平面DCC1D1,设BN=x,MN=y,则函数y=f(x)的图象大致是( )
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=2,AB=1,M、N分别在AD1,BC上移动,并始终保持MN∥平面DCC1D1,设BN=x,MN=y,则函数y=f(x)的图象大致是( )A、 | B、 | C、 | D、 |
在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=
,E为AB上一个动点,则D1E+CE的最小值为( )
| 3 |
A、2
| ||
B、
| ||
C、
| ||
| D、x≤y |
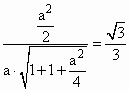 ,解得a=2,故点E的坐标为(1,1,1)(4分);
,解得a=2,故点E的坐标为(1,1,1)(4分);