题目内容
(本小题满分12分)
已知等比数列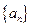 中,
中,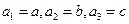 ,
,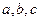 分别为
分别为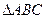 的三内角
的三内角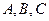 的对边,且
的对边,且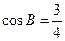 .
.
(1)求数列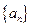 的公比
的公比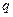 ;
;
(2)设集合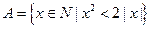 ,且
,且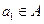 ,求数列
,求数列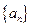 的通项公式.
的通项公式.
已知等比数列
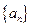 中,
中,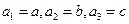 ,
,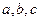 分别为
分别为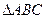 的三内角
的三内角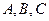 的对边,且
的对边,且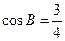 .
.(1)求数列
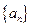 的公比
的公比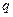 ;
;(2)设集合
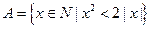 ,且
,且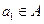 ,求数列
,求数列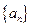 的通项公式.
的通项公式.(1)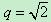 或
或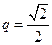
(2)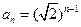 或
或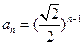
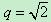 或
或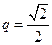
(2)
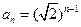 或
或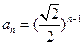
解:(1)依题意知: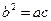 ,由余弦定理得:
,由余弦定理得:
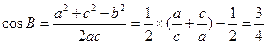 ,......3分
,......3分
而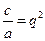 ,代入上式得
,代入上式得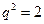 或
或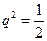 ,又在三角形中
,又在三角形中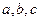
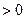 ,
,
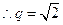 或
或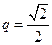 ;......6分
;......6分
(2)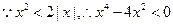 ,即
,即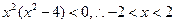 且
且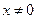 ,......9分
,......9分
又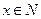 ,所以
,所以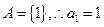 ,
,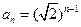 或
或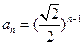 .......12分
.......12分
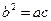 ,由余弦定理得:
,由余弦定理得: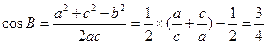 ,......3分
,......3分而
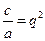 ,代入上式得
,代入上式得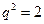 或
或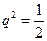 ,又在三角形中
,又在三角形中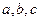
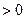 ,
,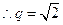 或
或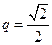 ;......6分
;......6分(2)
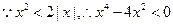 ,即
,即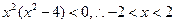 且
且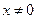 ,......9分
,......9分又
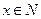 ,所以
,所以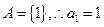 ,
,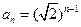 或
或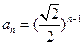 .......12分
.......12分
练习册系列答案
相关题目
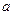
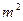 ,预计以后的10年中,人口的年增长率为
,预计以后的10年中,人口的年增长率为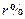 ,要想10年后
,要想10年后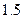 倍,试问这10年中,平均每年新建住房多少
倍,试问这10年中,平均每年新建住房多少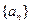 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且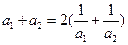 ,
,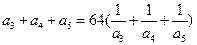
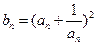 ,求数列
,求数列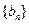 的前
的前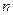 项和
项和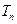 。
。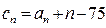 ,求数列{
,求数列{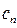 }的前
}的前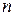 项和最小时
项和最小时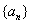 中,
中,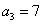 ,前3项之和
,前3项之和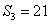 ,则数列
,则数列
 或
或
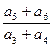 的值为 ( )
的值为 ( )


 中,
中, ,
, ,则
,则 的值为( )
的值为( )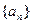 中,
中,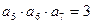 ,
,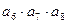 =24,则
=24,则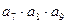 =" " ( )
=" " ( ) 的公比
的公比 前
前 项和为
项和为 若
若 则
则 ( )
( ) 



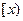 表示超过
表示超过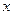 的最小整数,如
的最小整数,如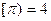 ,
,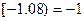 。有下列命题:①若函数
。有下列命题:①若函数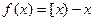 ,
,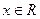 ,则值域为
,则值域为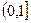 ;②若
;②若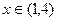 ,则方程
,则方程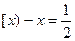 有三个根;③若
有三个根;③若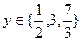 ,则
,则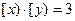 的概率
的概率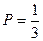 ;④如果数列
;④如果数列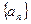 是等比数列,
是等比数列,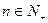 ,那么数列
,那么数列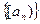 一定不是等比数列。其中正确的是
一定不是等比数列。其中正确的是