题目内容
已知抛物线y=-x2+3上存在关于直线x+y=0对称的相异两点A,B,则|AB|等于( )
| A.3 | B.4 | C.3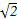 | D.4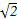 |
C
【思路点拨】转化为过A,B两点且与x+y=0垂直的直线与抛物线相交后求弦长问题求解.
设直线AB的方程为y=x+b,A(x1,y1),B(x2,y2),
由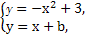 ⇒x2+x+b-3=0⇒x1+x2=-1,
⇒x2+x+b-3=0⇒x1+x2=-1,
得AB的中点M(- ,-
,- +b),
+b),
又M(- ,-
,- +b)在直线x+y=0上,可求出b=1,
+b)在直线x+y=0上,可求出b=1,
∴x2+x-2=0,
则|AB|=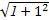 ·
·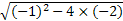 =3
=3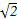 .
.
【方法技巧】对称问题求解技巧
若A,B两点关于直线l对称,则直线AB与直线l垂直,且线段AB的中点在直线l上,即直线l是线段AB的垂直平分线,求解这类圆锥曲线上的两点关于直线l的对称问题,常转化为过两对称点的直线与圆锥曲线的相交问题求解.
设直线AB的方程为y=x+b,A(x1,y1),B(x2,y2),
由
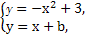 ⇒x2+x+b-3=0⇒x1+x2=-1,
⇒x2+x+b-3=0⇒x1+x2=-1,得AB的中点M(-
 ,-
,- +b),
+b),又M(-
 ,-
,- +b)在直线x+y=0上,可求出b=1,
+b)在直线x+y=0上,可求出b=1,∴x2+x-2=0,
则|AB|=
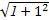 ·
·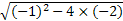 =3
=3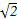 .
.【方法技巧】对称问题求解技巧
若A,B两点关于直线l对称,则直线AB与直线l垂直,且线段AB的中点在直线l上,即直线l是线段AB的垂直平分线,求解这类圆锥曲线上的两点关于直线l的对称问题,常转化为过两对称点的直线与圆锥曲线的相交问题求解.

练习册系列答案
相关题目
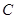 过定点(1,0),且与直线
过定点(1,0),且与直线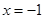 相切.
相切.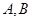 是轨迹
是轨迹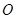 的两个不同点,直线
的两个不同点,直线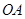 和
和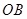 的倾斜角分别为
的倾斜角分别为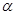 和
和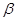 ,①当
,①当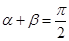 时,求证直线
时,求证直线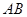 恒过一定点
恒过一定点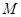 ;
;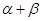 为定值
为定值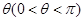 ,直线
,直线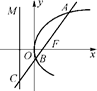
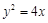 上运动,F为抛物线的焦点,点M的坐标为(3,2),当PM+PF取最小值时点P的坐标为 .
上运动,F为抛物线的焦点,点M的坐标为(3,2),当PM+PF取最小值时点P的坐标为 .