题目内容
设A、B、C、D是半径为2的球面上的四点,且满足AB⊥AC,AD⊥AC,AB⊥AD,则S△ABC+S△ABD+S△ACD的最大值是
8
8
.分析:根据题意,以AB、AC、AD为长、宽、高作长方体,可得长方体与三棱锥D-ABC有相同的外接球.从而算出长方体的对角线长为4,得AB2+AC2+AD2=16.再利用基本不等式求最值即可算出S△ABC+S△ABD+S△ACD的最大值.
解答:解: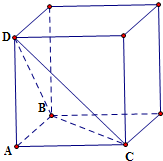 ∵AB⊥AC,AD⊥AC,AB⊥AD,
∵AB⊥AC,AD⊥AC,AB⊥AD,
∴以AB、AC、AD为长、宽、高,作长方体如图所示
可得长方体的外接球就是三棱锥D-ABC的外接球
∵球的半径为2,可得直径为4
∴长方体的对角线长为4,得AB2+AC2+AD2=16
∵S△ABC=
AB•AC,S△ABD=
AB•AD,S△ACD=
AC•AD
∴S△ABC+S△ABD+S△ACD=
(AB•AC+AB•AD+AC•AD)
∵AB•AC+AB•AD+AC•AD≤AB2+AC2+AD2=16
当且仅当AB=AC=AD时,等号成立
∴当且仅当AB=AC=AD时,S△ABC+S△ABD+S△ACD的最大值为8
故答案为:8
 ∵AB⊥AC,AD⊥AC,AB⊥AD,
∵AB⊥AC,AD⊥AC,AB⊥AD,∴以AB、AC、AD为长、宽、高,作长方体如图所示
可得长方体的外接球就是三棱锥D-ABC的外接球
∵球的半径为2,可得直径为4
∴长方体的对角线长为4,得AB2+AC2+AD2=16
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABC+S△ABD+S△ACD=
| 1 |
| 2 |
∵AB•AC+AB•AD+AC•AD≤AB2+AC2+AD2=16
当且仅当AB=AC=AD时,等号成立
∴当且仅当AB=AC=AD时,S△ABC+S△ABD+S△ACD的最大值为8
故答案为:8
点评:本题求内接于球的三棱锥的侧面积的最大值,着重考查了球内接多面体、长方体的性质和基本不等式求最值等知识,属于中档题.

练习册系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题纸指定区域内 作答.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题纸指定区域内 作答.解答应写出文字说明、证明过程或演算步骤. [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.