题目内容
函数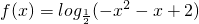 的单调增区间是________.
的单调增区间是________.
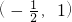
分析:先求出函数f(x)的定义域,然后把函数f(x)分解为两基本函数y=
 和t=-x2-x+2,根据复合函数单调性的判定方法只需在定义域内求出t=-x2-x+2的减区间即可.
和t=-x2-x+2,根据复合函数单调性的判定方法只需在定义域内求出t=-x2-x+2的减区间即可.解答:由-x2-x+2>0,得-2<x<1,即函数f(x)的定义域为(-2,1).
函数f(x)可看作由函数y=
 和t=-x2-x+2复合而成的,
和t=-x2-x+2复合而成的,函数y=
 单调递减,
单调递减,由复合函数单调性的判定方法知,要求f(x)的增区间只需求出t=-x2-x+2的减区间.
而t=-x2-x+2=-
 +
+ 的减区间是(-
的减区间是(- ,1).
,1).所以函数f(x)的单调增区间是(-
 ,1).
,1).故答案为:(-
 ,1).
,1).点评:本题考查复合函数单调区间的求解及对数函数的单调性问题,该类问题一要注意考虑函数定义域,二要理解复合函数单调性的判定方法:同增异减.

练习册系列答案
相关题目
 的单调增区间是
的单调增区间是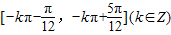 .
. 的图象,需把函数y=sinx的图象上所有点向左平行移动
的图象,需把函数y=sinx的图象上所有点向左平行移动 个单位长度.
个单位长度. .
. 的单调增区间是 .
的单调增区间是 . 的单调增区间是
的单调增区间是 B.
B. C.
C. D.
D.
 的单调增区间是___________________________。
的单调增区间是___________________________。