题目内容
已知函数 ,若|f(x)|≥ax,则a的取值范围是( )
,若|f(x)|≥ax,则a的取值范围是( )
| A.(-∞,0] | B.(-∞,1] |
| C.[-2,1] | D.[-2,0] |
D
解析函数y=|f(x)|的图象如图.
①当a=0时,|f(x)|≥ax显然成立.
②当a>0时,只需在x>0时,
ln(x+1)≥ax成立.
比较对数函数与一次函数y=ax的增长速度.
显然不存在a>0使ln(x+1)≥ax在x>0上恒成立.
③当a<0时,只需在x<0时,x2-2x≥ax成立.
即a≥x-2成立,∴a≥-2.
综上所述:-2≤a≤0.故选D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数 的零点有( )
的零点有( )
| A.0个 |
| B.1个 |
| C.2个 |
| D.3个 |
有一段“三段论”推理是这样的:“对于可导函数 ,如果
,如果 ,那么
,那么 是函数
是函数 的极值点;因为函数
的极值点;因为函数 在
在 处的导数值
处的导数值 ,所以
,所以 是函数
是函数 的极值点.”以上推理中( )
的极值点.”以上推理中( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
下列函数中,既是偶函数又在 上单调递增的是( )
上单调递增的是( )
A. | B. | C. | D. |
若 ,则函数
,则函数 的两个零点分别位于区间( )
的两个零点分别位于区间( )
| A.(a,b)和(b,c)内 |
| B.(-∞,a)和(a,b)内 |
| C.(b,c)和(c,+∞)内 |
| D.(-∞,a)和(c,+∞)内 |
函数f(x)=(x-3)ex的单调递增区间是( )
| A.(-∞,2) |
| B.(0,3) |
| C.(1,4) |
| D.(2,+∞) |
函数 的定义域为( )
的定义域为( )
A.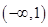 |
B. |
C. |
D.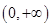 |
设函数 定义在实数集R上,
定义在实数集R上, ,且当
,且当 时
时 =
= ,则有 ( )
,则有 ( )
A.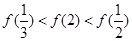 |
B. |
C. |
D. |
 的图象大致是( ).
的图象大致是( ).