题目内容
关于x的不等式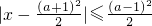 与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A⊆B的a的取值范围.
与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A⊆B的a的取值范围.
 解:由关于x的不等式
解:由关于x的不等式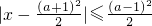 ,可得-
,可得-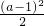 ≤x-
≤x-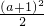 ≤
≤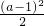 ,解得 2a≤x≤a2-1,
,解得 2a≤x≤a2-1,∴A=[2a,a2-1].
解不等式x2-3(a+1)x+2(3a+1)≤0可得,(x-2)[x-(3a+1)]≤0,∴B={x|(x-2)[x-(3a+1)]≤0},
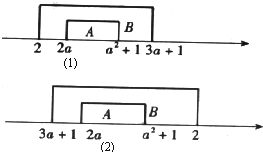
由A⊆B,如图所示:
可得
 ,或
,或 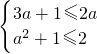 .
.解得 1≤a≤3,或 a=-1,故a的取值范围为 {a|1≤a≤3,或 a=-1 }.
分析:解绝对值不等式求得A=[2a,a2-1],解一元二次不等式求得B={x|(x-2)[x-(3a+1)]≤0},由A⊆B,可得
 ,或
,或 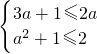 .分别求得这两个
.分别求得这两个不等式组的解集,再取并集,即得所求.
点评:本题主要考查绝对值不等式的解法,一元二次不等式的解法,集合间的包含关系,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
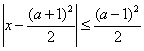
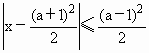 与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A
与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A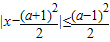 与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A⊆B的a的取值范围.
与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A⊆B的a的取值范围.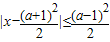 与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A⊆B的a的取值范围.
与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A⊆B的a的取值范围.