题目内容
关于x的不等式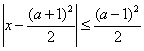 与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A
与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A![]() B的a的取值范围.
B的a的取值范围.
答案:
解析:
解析:
由 得 即2a≤x≤a2+1 ∴ A={x|2a≤x≤a2+1} 又不等式x2-3(a+1)x+2(3a+1)≤0 可化为(x-2)[x-(3a+1)]≤0 ∴ B={x|(x-2)[x-(3a+1)]≤0} 解法一:由于A
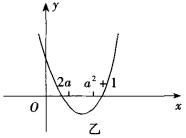
∴ 故a的取值范围是{a|1≤a≤3或a=-1} 解法二:如图乙所示我们构造函数图像设 f(x)=x2-3(a+1)x+2(3a+1) ∵A
即 ∴ ∴ 1≤a≤3或a=-1 故a的取值范围是{a|1≤a≤3或a=-1}. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
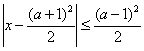
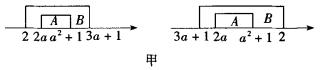
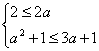 或
或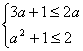
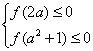
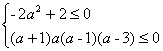
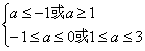
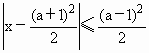 与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A
与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A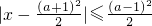 与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A⊆B的a的取值范围.
与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A⊆B的a的取值范围.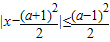 与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A⊆B的a的取值范围.
与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A⊆B的a的取值范围.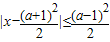 与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A⊆B的a的取值范围.
与x2-3(a+1)x+2(3a+1)≤0(a∈R)的解集分别是A和B,求使A⊆B的a的取值范围.