题目内容
抛物线的顶点在原点,焦点在射线x-y+1=0(x≥0)上
(1)求抛物线的标准方程
(2)过(1)中抛物线的焦点F作动弦AB,过A、B两点分别作抛物线的切线,设其交点为M,求点M的轨迹方程,并求出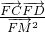 的值.
的值.
解:(1)∵是标准方程,∴其焦点应该在坐标轴上,
∴令x=0,代入射线x-y+1=0,解得其焦点坐标为(0,1)
当焦点为(0,1)时,可知P=2,∴其方程为x2=4y.
(2)设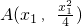 ,
,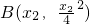
过抛物线A,B两点的切线方程分别是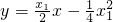 ,
,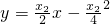
其交点坐标
设AB的直线方程y=kx+1代入x2=4y,得x2-4kx-4=0
∴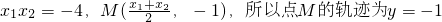
∵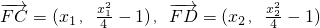
∴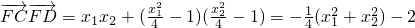
而
∴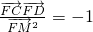 .
.
分析:(1)先射线x-y+1=0(x≥0)与坐标轴的交点解得焦点坐标,根据抛物线的焦点坐标,求出抛物线的标准方程.
(2)设AB的直线方程y=kx+1,将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量数量积的坐标运算公式即可求出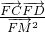 的值,从而解决问题.
的值,从而解决问题.
点评:本题主要考查平面向量数量积的运算、抛物线的标准方程.抛物线的标准方程的焦点一定在坐标轴上且定点一定在原点,即先确定焦点的坐标再求出标准方程.
∴令x=0,代入射线x-y+1=0,解得其焦点坐标为(0,1)
当焦点为(0,1)时,可知P=2,∴其方程为x2=4y.
(2)设
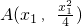 ,
,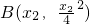
过抛物线A,B两点的切线方程分别是
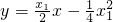 ,
,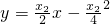
其交点坐标

设AB的直线方程y=kx+1代入x2=4y,得x2-4kx-4=0
∴
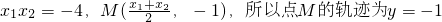
∵
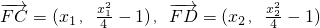
∴
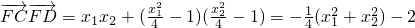
而

∴
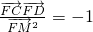 .
.分析:(1)先射线x-y+1=0(x≥0)与坐标轴的交点解得焦点坐标,根据抛物线的焦点坐标,求出抛物线的标准方程.
(2)设AB的直线方程y=kx+1,将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量数量积的坐标运算公式即可求出
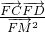 的值,从而解决问题.
的值,从而解决问题.点评:本题主要考查平面向量数量积的运算、抛物线的标准方程.抛物线的标准方程的焦点一定在坐标轴上且定点一定在原点,即先确定焦点的坐标再求出标准方程.

练习册系列答案
相关题目
设抛物线的顶点在原点,准线方程为x=-2,则抛物线的方程是( )
| A、y2=-8x | B、y2=8x | C、y2=-4x | D、y2=4x |
 (2012•江苏一模)本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.
(2012•江苏一模)本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力. 实轴长为
实轴长为