题目内容
以下4个命题:
1)三个点可以确定一个平面;
2)平行于同一个平面的两条直线平行;
3)抛物线y2=-4x对称轴为y轴;
4)同时垂直于一条直线的两条直线一定平行;
正确的命题个数为
1)三个点可以确定一个平面;
2)平行于同一个平面的两条直线平行;
3)抛物线y2=-4x对称轴为y轴;
4)同时垂直于一条直线的两条直线一定平行;
正确的命题个数为
0
0
.分析:1)由平面的性质可得:三个不共线的点可以确定一个平面.
2)由空间中的两条直线的位置关系可得:这两条直线可能平行、可能异面、可能相交.
3)由抛物线的性质可得:抛物线y2=-4x对称轴为x轴.
4)空间中的两条直线的位置关系可得:这两条直线可能平行、可能异面、可能相交.
2)由空间中的两条直线的位置关系可得:这两条直线可能平行、可能异面、可能相交.
3)由抛物线的性质可得:抛物线y2=-4x对称轴为x轴.
4)空间中的两条直线的位置关系可得:这两条直线可能平行、可能异面、可能相交.
解答:解:1)由平面的性质可得:三个不共线的点可以确定一个平面,所以1)错误.
2)由空间中的两条直线的位置关系可得:平行于同一个平面的两条直线可能平行、可能异面、可能相交,所以2)错误.
3)由抛物线的性质可得:抛物线y2=-4x对称轴为x轴,所以3)错误.
4)空间中的两条直线的位置关系可得:在空间中同时垂直于一条直线的两条直线可能平行、可能异面、可能相交,所以4)错误.
故答案为:0.
2)由空间中的两条直线的位置关系可得:平行于同一个平面的两条直线可能平行、可能异面、可能相交,所以2)错误.
3)由抛物线的性质可得:抛物线y2=-4x对称轴为x轴,所以3)错误.
4)空间中的两条直线的位置关系可得:在空间中同时垂直于一条直线的两条直线可能平行、可能异面、可能相交,所以4)错误.
故答案为:0.
点评:本题主要考查平面的定义与空间中点、线、面之间的位置关系,以及抛物线的有关性质,此题属于基础题.

练习册系列答案
相关题目
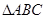 中, “
中, “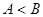 ”是“
”是“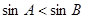 ”的必要而非充分条件;
”的必要而非充分条件;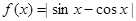 的最小正周期是
的最小正周期是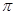 ;
;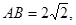
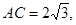
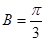 ,则
,则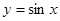 与函数
与函数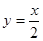 的图象有三个交点
的图象有三个交点 B.
2 C.
3
D. 4
B.
2 C.
3
D. 4