题目内容
5.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左右焦点分别为F1,F2,O为双曲线的中心,P是双曲线右支上的点,△PF1F2的内切圆的圆心为I,且圆I与x轴相切于点A,过F2作直线PI的垂线,垂足为B,若e为双曲线的离心率,则( )| A. | |OB|=|OA| | B. | |OA|=e|OB| | ||
| C. | |OB|=e|OA| | D. | |OB|与|OA|大小关系不确定 |
分析 根据题意,利用切线长定理,再利用双曲线的定义,把|PF1|-|PF2|=2a,转化为|AF1|-|AF2|=2a,从而求得点H的横坐标.再在三角形PCF2中,由题意得,它是一个等腰三角形,从而在三角形F1CF2中,利用中位线定理得出OB,从而解决问题.
解答 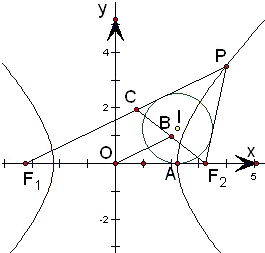 解:F1(-c,0)、F2(c,0),内切圆与x轴的切点是点A
解:F1(-c,0)、F2(c,0),内切圆与x轴的切点是点A
∵|PF1|-|PF2|=2a,及圆的切线长定理知,
|AF1|-|AF2|=2a,设内切圆的圆心横坐标为x,
则|(x+c)-(c-x)|=2a
∴x=a;
|OA|=a,
在△PCF2中,由题意得,F2B⊥PI于B,延长交F1F2于点C,利用△PCB≌△PF2B,可知PC=PF2,
∴在三角形F1CF2中,有:
OB=$\frac{1}{2}$CF1=$\frac{1}{2}$(PF1-PC)=$\frac{1}{2}$(PF1-PF2)=$\frac{1}{2}$×2a=a.
∴|OB|=|OA|.
故选:A.
点评 本题考查双曲线的定义、切线长定理.解答的关键是充分利用平面几何的性质,如三角形内心的性质等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.用均匀随机数进行随机模拟,可以解决( )
| A. | 只能求几何概型的概率,不能解决其他问题 | |
| B. | 不仅能求几何概型的概率,还能计算图形的面积 | |
| C. | 不但能估计几何概型的概率,还能估计图形的面积 | |
| D. | 最适合估计古典概型的概率 |
10.某市工业部门计划对所辖中小型工业企业推行节能降耗技术改造,对所辖企业是否支持改造进行问卷调查,结果如表:
(Ⅰ)能否在犯错误的概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关?
(Ⅱ)从上述320家支持节能降耗改造的中小企业中按分层抽样的方法抽出8家,然后从这8家中选出2家,求这2家中恰好中、小型企业各一家的概率
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(b+d)}$
| 支持 | 不支持 | 合计 | |
| 中型企业 | 80 | 40 | 120 |
| 小型企业 | 240 | 200 | 440 |
| 合计 | 320 | 240 | 560 |
(Ⅱ)从上述320家支持节能降耗改造的中小企业中按分层抽样的方法抽出8家,然后从这8家中选出2家,求这2家中恰好中、小型企业各一家的概率
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(b+d)}$
| P(K2≥k0) | 0.050 | 0.025 | 0.010 |
| K0 | 3.841 | 5.024 | 6.635 |