题目内容
已知中心为坐标原点、对称轴为坐标轴的双曲线C经过椭圆
+
=1的焦点,且双曲线C的焦点到其渐近线的距离为1,则该双曲线的渐近线方程为( )
| x2 |
| 9 |
| y2 |
| 5 |
分析:求出椭圆
+
=1的焦点坐标,可得双曲线的顶点坐标,利用双曲线C的焦点到其渐近线的距离为1,求出a,从而可求该双曲线的渐近线方程.
| x2 |
| 9 |
| y2 |
| 5 |
解答:解:由题意,椭圆
+
=1的焦点坐标为(±2,0),
∵中心为坐标原点、对称轴为坐标轴的双曲线C经过椭圆
+
=1的焦点,
∴双曲线的顶点坐标为(±2,0),
设双曲线的焦点坐标为(±c,0),渐近线方程为y=±
x,即bx±ay=0.
∴焦点到其渐近线的距离为
=b=1,
∵a=2,
∴双曲线的渐近线方程为y=±
x=±
x.
故选B.
| x2 |
| 9 |
| y2 |
| 5 |
∵中心为坐标原点、对称轴为坐标轴的双曲线C经过椭圆
| x2 |
| 9 |
| y2 |
| 5 |
∴双曲线的顶点坐标为(±2,0),
设双曲线的焦点坐标为(±c,0),渐近线方程为y=±
| b |
| a |
∴焦点到其渐近线的距离为
| bc | ||
|
∵a=2,
∴双曲线的渐近线方程为y=±
| b |
| a |
| 1 |
| 2 |
故选B.
点评:本题考查椭圆、双曲线的几何性质,考查点到直线距离公式的运用,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
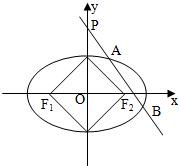 已知中心为坐标原点O,焦点在x轴上的椭圆的两个短轴端点和左右焦点所组成的四边形是面积为2的正方形,
已知中心为坐标原点O,焦点在x轴上的椭圆的两个短轴端点和左右焦点所组成的四边形是面积为2的正方形,

