题目内容
平行六面体ABCD-A1B1C1D1的六个面都是菱形，则点D1在面ACB1上的射影是△ACB1 的（ ）A．外心
B．内心
C．垂心
D．重心
【答案】分析：根据菱形的对角线互相垂直，及三垂线定理与逆定理，可证明线段垂直，从而证明射影是垂心
解答：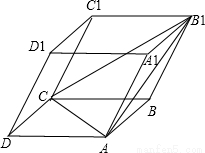
证明：如图：设点D1在面ACB1中的射影为点M，连接B1D1、B1M
则B1M是B1D1在面ACB1中的射影
∵该平行六面体各个表面都是菱形
∴AC∥A1C1，B1D1⊥A1C1
∴B1D1⊥AC
∴由三垂线定理知B1M⊥AC
同理可证AM⊥B1C，CM⊥AB1
∴点M是△ACB1的垂心
故选C
点评：本题考察三垂线定理的应用，由三垂线定理可证明线线垂直，及菱形的性质特点，属较难题
解答：
证明：如图：设点D1在面ACB1中的射影为点M，连接B1D1、B1M则B1M是B1D1在面ACB1中的射影
∵该平行六面体各个表面都是菱形
∴AC∥A1C1，B1D1⊥A1C1
∴B1D1⊥AC
∴由三垂线定理知B1M⊥AC
同理可证AM⊥B1C，CM⊥AB1
∴点M是△ACB1的垂心
故选C
点评：本题考察三垂线定理的应用，由三垂线定理可证明线线垂直，及菱形的性质特点，属较难题
练习册系列答案
综合自测系列答案
相关题目
如图，已知平行六面体ABCD-A1B1C1D1（底面是平行四边形的四棱柱）
如图已知平行六面体ABCD-A′B′C′D′，E、F、G、H分别是棱A′D′、D′C′、C′C和AB的中点，求证E、F、G、H四点共面．
如图，在平行六面体ABCD-A1B1C1D1中，底面是边长为1的正方形，若