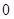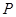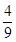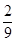题目内容
在一个盒子中,放有标号分别为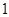 ,
, ,
,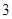 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为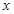 、
、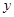 ,记
,记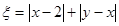 .
.
(Ⅰ)求随机变量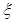 的最大值,并求事件“
的最大值,并求事件“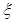 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求随机变量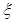 的分布列和数学期望.
的分布列和数学期望.
【答案】
(Ⅰ)随机变量 的最大值为
的最大值为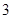 ,
,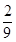 (Ⅱ)分布列见解析,数学期望为
(Ⅱ)分布列见解析,数学期望为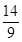
【解析】本题考查离散型随机变量的期望与方差,解题的关键是求出分布列,熟练掌握概率的求法公式是准确得出分布列的关键,本题知识性较强,考查到了求概率,求分布列,求期望,是概率中一个典型题,题后要总结其解题脉络.
(I)由题意x,y可能的取值为2、3、4由此可得出,|x-3|≤1,|y-x|≤2,即可得ξ≤3,分析出变量ξ的最大值时x,y的值,计算出事件“ξ取得最大值”包含的基本事件种数,由公式算出概率.
(Ⅱ)ξ的所有 取值为0,1,2,3,分别计算出ξ取每一个值时概率,列出分布列,由公式计算出数学期望。
解 (Ⅰ)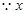 、
、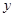 可能的取值为
可能的取值为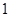 、
、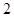 、
、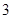 ,
,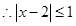 ,
,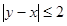 ,
,
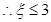 ,且当
,且当 或
或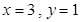 时,
时,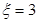 .
.
因此,随机变量 的最大值为
的最大值为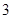 .
. 有放回抽两张卡片的所有情况有
有放回抽两张卡片的所有情况有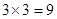 种,
种,
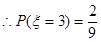 .
.
(Ⅱ) 的所有取值为
的所有取值为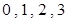 .
.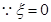 时,只有
时,只有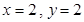 这一种情况,
这一种情况,
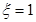 时,有
时,有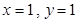 或
或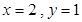 或
或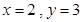 或
或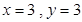 四种情况,
四种情况,
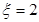 时,有
时,有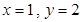 或
或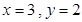 两种情况.
两种情况.
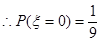 ,
,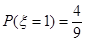 ,
,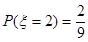 .
.
则随机变量 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
因此,数学期望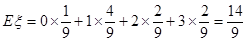 .
.

练习册系列答案
相关题目