题目内容
在一个盒子里放有6张卡片,上面标有数字1,2,3,4,5,6,现在从盒子里每次任意取出一张卡片,取两片.
(I)若每次取出后不再放回,求取到的两张卡片上数字之积大于12的概率;
(II)在每次取出后再放回和每次取出后不再放回这两种取法中,得到的两张卡片上的最大数字的期望值是否相等?请说明理由.
【答案】
(I)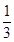 (II)不相等。理由见解析
(II)不相等。理由见解析
【解析】本试题主要是考查了概率中又放回的抽取和不放回抽取的概率的运用。
(1)不放回 抽取为古典概型取到的两张卡片上数字之积大于12的事件为3,4,5,6四个数中取出两个,且应除去3,4两个数字。
故所求事件概率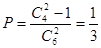
(2)又放回的是独立事件的概率,每次取出后再放回,则得到的两张卡片上的数字中最大数字是随机变量,η,η=1,2,3,4,5,6.
求解各个取值的概率值得到结论。
解:(I)取到的两张卡片上数字之积大于12的事件为3,4,5,6四个数中取出两个,且应除去3,4两个数字。
故所求事件概率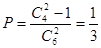 .
---------3分
.
---------3分
(II)若每次取出后不再放回,则得到的两张卡片上的数字中最大数字随机变量ξ,ξ=2,3,4,5,6.
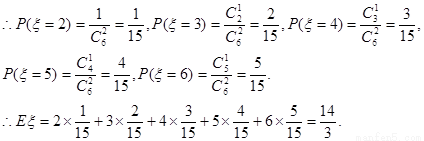
------7分
若每次取出后再放回,则得到的两张卡片上的数字中最大数字是随机变量,η,
η=1,2,3,4,5,6.
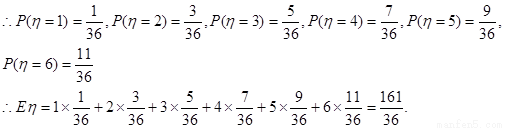 11分
11分
∴在每次取出后再放回和每次取出后不再取回这两种取法中,得到的两张卡上的数字中最大数字的期望值不相等. -----12分

练习册系列答案
相关题目