题目内容
判断一次函数y=kx+b反比例函数y=
,二次函数y=ax2+bx+c的单调性.
| k | x |
分析:分k>0,和k<0两种情况,分别讨论y=kx+b、y=
在其定义域内的单调性,分a>0和a<0两种情况,讨论二次函数y=ax2+bx+c的单调性.
| k |
| x |
解答:解:当k>0,y=kx+b在R是增函数,当k<0,y=kx+b在R是减函数;
当k>0,y=
在(-∞,0)、(0,+∞)上是减函数,
当k<0,y=
在(-∞,0)、(0,+∞)上是增函数;
当a>0,二次函数y=ax2+bx+c在(-∞-
)是减函数,在[-
+∞)上是增函数,
当a<0,二次函数y=ax2+bx+c在(-∞-
)是增函数,在[-
+∞)上是减函数.
当k>0,y=
| k |
| x |
当k<0,y=
| k |
| x |
当a>0,二次函数y=ax2+bx+c在(-∞-
| b |
| 2a |
| b |
| 2a |
当a<0,二次函数y=ax2+bx+c在(-∞-
| b |
| 2a |
| b |
| 2a |
点评:本题主要考查一次函数、二次函数、反比例函数的单调性的判断,属于基础题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 ;
;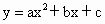 .
. ,二次函数y=ax2+bx+c的单调性.
,二次函数y=ax2+bx+c的单调性. ,二次函数y=ax2+bx+c的单调性.
,二次函数y=ax2+bx+c的单调性.