��Ŀ����
 ��һ���壬������Ϊ���ư����Բ����ͼ������Բ����˵�ΪA��B��AB�����Ϊ3km����Բ����ΪC��D��CD�����Ϊ2km����C��D���ֱ��мף��������;��������ں������Ͻ�һ�ȼٴ�P�������Ƿ��������Ӱ�죬�;��Զȼٴ������Ⱦ�̶����ų�������Ũ�ȳ����ȣ�����ϵ����Ϊk1����������ƽ���ɷ��ȣ�����ϵ����Ϊk2������֪���;��ų��ķ���Ũ�����ҵ�8����
��һ���壬������Ϊ���ư����Բ����ͼ������Բ����˵�ΪA��B��AB�����Ϊ3km����Բ����ΪC��D��CD�����Ϊ2km����C��D���ֱ��мף��������;��������ں������Ͻ�һ�ȼٴ�P�������Ƿ��������Ӱ�죬�;��Զȼٴ������Ⱦ�̶����ų�������Ũ�ȳ����ȣ�����ϵ����Ϊk1����������ƽ���ɷ��ȣ�����ϵ����Ϊk2������֪���;��ų��ķ���Ũ�����ҵ�8������1�������;��ų���Ũ��Ϊa��aΪ�������ȼٴ�P������;�xkm���ȼٴ�P�ܵ��������;�����Ⱦ�̶Ⱥͼ�Ϊf��x������f��x���ı���ʽ��������
��2���ȼٴ�P������;�����ʱ���������;��Զȼٴ�ķ�����Ⱦ�̶Ⱥ���С��
��������1���ɵ�P����Բ�ϣ�֪|PC|+|PD|=3����|PC|=x����|PD|=3-x���ɴ˿ɵ�P���ܼ��;���Ⱦ�̶ȡ������;���Ⱦ�̶ȣ����������Ⱦ�̶Ⱥͣ�
��2����f(x)=
+
=ak1k2��
+
����������ȷ�������ĵ����ԣ��Ӷ�����������Сֵ��
��2����f(x)=
| 8ak1k2 |
| x2 |
| ak1k2 |
| (3-x)2 |
| 8 |
| x2 |
| 1 |
| 9-6x+x2 |
����⣺��1���ɵ�P����Բ�ϣ�֪|PC|+|PD|=3����|PC|=x����|PD|=3-x��
P���ܼ��;���Ⱦ�̶�Ϊ
��P�������;���Ⱦ�̶�Ϊ
��Ⱦ�̶Ⱥ�Ϊf(x)=
+
��������Ϊ[
��
]
��2����f(x)=
+
=ak1k2��
+
����
�������ɵ�f�䣨x��=18ak1k2��
��f�䣨x��=0�����x=2��
��x��(
��2)ʱ��f�䣨x����0������Ϊ����������x(2��
)ʱ��f�䣨x����0������Ϊ��������
��x=2ʱ��f��x��ȡ����Сֵ��
�𣬶ȼٴ������;�2kmʱ���ס������;��Զȼٴ�ķ�����Ⱦ�̶Ⱥ���С��
P���ܼ��;���Ⱦ�̶�Ϊ
| 8ak1k2 |
| x2 |
| ak1k2 |
| (3-x)2 |
��Ⱦ�̶Ⱥ�Ϊf(x)=
| 8ak1k2 |
| x2 |
| ak1k2 |
| (3-x)2 |
| 1 |
| 2 |
| 5 |
| 2 |
��2����f(x)=
| 8ak1k2 |
| x2 |
| ak1k2 |
| (3-x)2 |
| 8 |
| x2 |
| 1 |
| 9-6x+x2 |
�������ɵ�f�䣨x��=18ak1k2��
| (x-2)(x2-6x+12) |
| x3(3-x)3 |
��f�䣨x��=0�����x=2��
��x��(
| 1 |
| 2 |
| 5 |
| 2 |
��x=2ʱ��f��x��ȡ����Сֵ��
�𣬶ȼٴ������;�2kmʱ���ס������;��Զȼٴ�ķ�����Ⱦ�̶Ⱥ���С��
���������⿼�鵼����Ӧ�ã����麯��˼�룬�����Ķ���������ģ���������������������е��⣮

��ϰ��ϵ�д�
�����Ŀ

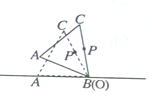 ��ͼ����ˮƽ��������һ��������ľ���Ϊ��ABC�߳�Ϊ1����PΪBC���е㣬�ֶԡ�ABC������ˮƽ������˶���
��ͼ����ˮƽ��������һ��������ľ���Ϊ��ABC�߳�Ϊ1����PΪBC���е㣬�ֶԡ�ABC������ˮƽ������˶���