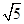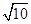题目内容
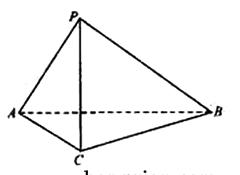
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
(Ⅰ)求证:PC⊥AB;
(Ⅱ)求直线BC与平面APB所成角的正弦值
(Ⅲ)求点C到平面APB的距离.

(Ⅰ)求证:PC⊥AB;
(Ⅱ)求直线BC与平面APB所成角的正弦值
(Ⅲ)求点C到平面APB的距离.
(I) 取AB中点D,连结PD,CD.
∵AP=BP,
∴PD⊥AB. ……………1
∵AC=BC,
∴CD⊥AB. ……………2
∵PD∩CD=D,
∴AB⊥平面PCD. ……………3
∵PC∩平面PCD.
∴PC⊥AB. ……………4
(Ⅱ)∵AC=BC,AP=BP,
∴△APC≌△BPC.
又PC⊥BC.
∴PC⊥BC.
又∠ACB=90°,即AC⊥BC.
且AC∩PC=C,
∴BC⊥平面PAC.
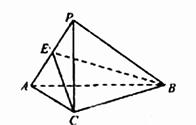
取AP中点E,连结BE,CE.
∵AB=BP,
∴BE⊥AP.
∵EC是BE在平面PAC内的射影.
∴CE⊥AP.
∴∠EBC是直线BC与平面APB所成的角 ……………6
在△BCE中,∠BCE=90°,BC=2,BE=
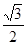 AB=
AB=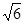 ,
,sin∠EBC=
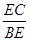 =
=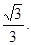 ……………8
……………8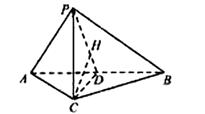
(Ⅲ)由(Ⅰ)知AB⊥平面PCD,
∴平面APB⊥平面PCD.
过C作CH⊥PD,垂足为H.
∵平面APB∩平面PCD=PD,
∴CH⊥平面APB.
∴CH的长即为点C到平面APB的距离, ……………10
由(Ⅰ)知PC⊥AB,又PC⊥AC,
且AB∩AC=A.
∴PC⊥平面ABC.
CD
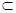 平面ABC.
平面ABC.∴PC⊥CD.
在Rt△PCD中,CD=
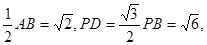
∴PC=
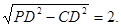
∴CH=
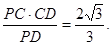
∴点C到平面APB的距离为
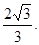
略

练习册系列答案
相关题目
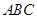 的底边
的底边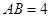 ,点
,点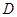 在线段
在线段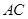 上,
上,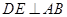 于
于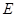 ,现将
,现将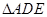 沿
沿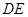 折起到
折起到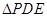 的位置(如图(2)).
的位置(如图(2)).
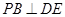 ;
;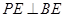 ,直线
,直线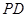 与平面
与平面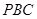 所成的角为
所成的角为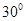 ,求
,求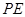 长.
长.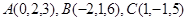 ,则以AB,AC为边的平行四边形的面积____
,则以AB,AC为边的平行四边形的面积____ 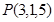 关于
关于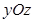 平面对称的点的坐标为( )
平面对称的点的坐标为( )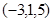
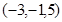
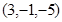
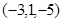
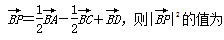
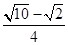
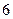 ;
;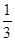
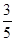

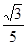
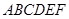 中,
中,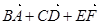
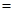 ( )
( )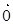
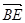
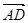
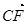
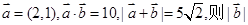 = ( ▲)
= ( ▲)