题目内容
设函数f(x)=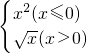 ,若f(x0)>1,则x0的取值范围是
,若f(x0)>1,则x0的取值范围是
- A.(-1,1)
- B.(-1,+∞)
- C.(-∞,-2)∪(0,+∞)
- D.(-∞,-1)∪(1,+∞)
D
分析:根据已知中f(x)=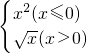 是一个分段函数,故我们可分x≤0和x>0两种情况,分别求出f(x)>1时,x的取值范围,综合讨论结果可得答案.
是一个分段函数,故我们可分x≤0和x>0两种情况,分别求出f(x)>1时,x的取值范围,综合讨论结果可得答案.
解答:当x≤0时,
若f(x)=x2>1,则x<-1
当x>0时,
若f(x)= >1,则x>1
>1,则x>1
综上若f(x0)>1,则x0的取值范围是(-∞,-1)∪(1,+∞)
故选D
点评:本题考查的知识点分段函数,分段不等式的解法,分段函数分段处理,是解答此类问题的不二法门
分析:根据已知中f(x)=
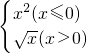 是一个分段函数,故我们可分x≤0和x>0两种情况,分别求出f(x)>1时,x的取值范围,综合讨论结果可得答案.
是一个分段函数,故我们可分x≤0和x>0两种情况,分别求出f(x)>1时,x的取值范围,综合讨论结果可得答案.解答:当x≤0时,
若f(x)=x2>1,则x<-1
当x>0时,
若f(x)=
 >1,则x>1
>1,则x>1综上若f(x0)>1,则x0的取值范围是(-∞,-1)∪(1,+∞)
故选D
点评:本题考查的知识点分段函数,分段不等式的解法,分段函数分段处理,是解答此类问题的不二法门

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目