题目内容
已知函数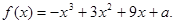
(Ⅰ)求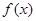 的单调减区间;
的单调减区间;
(Ⅱ)若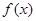 在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
【解析】(1)求导令导数小于零.
(2)利用导数列表求极值,最值即可.
【答案】
解:(I) 令
令 ,解得
,解得
所以函数 的单调递减区间为
的单调递减区间为
(II)因为

所以 因为在(-1,3)上
因为在(-1,3)上 ,所以
,所以 在[-1,2]上单调递增,又由于
在[-1,2]上单调递增,又由于 在[-2,-1]上单调递减,因此
在[-2,-1]上单调递减,因此 和
和 分别是
分别是 在区间[-2,2]上的最大值和最小值.于是有
在区间[-2,2]上的最大值和最小值.于是有 ,解得
,解得
故 因此
因此
即函数 在区间[-2,2]上的最小值为-7.
在区间[-2,2]上的最小值为-7.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 ,
,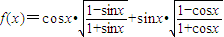
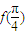 的值;
的值;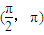 上的单调区间和值域.
上的单调区间和值域.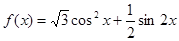 .
. 的最小正周期;
的最小正周期;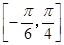 上的最大值和最小值.
上的最大值和最小值.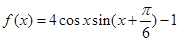 。
。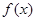 的最小正周期:
的最小正周期: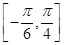 上的最大值和最小值。
上的最大值和最小值。