题目内容
 如图,已知椭圆的中心在原点,焦点在x轴上,离心率为
如图,已知椭圆的中心在原点,焦点在x轴上,离心率为 ,且经过点M(4,1).直线l:y=x+m交椭圆于A,B两不同的点.
,且经过点M(4,1).直线l:y=x+m交椭圆于A,B两不同的点.
(1)求椭圆的方程;
(2)当|AB|=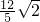 时,求m的值;
时,求m的值;
(3)若直线l不过点M,求证:直线MA,MB与x轴围成一个等腰三角形.
解:(1)设椭圆方程为
因为 所以a=2b
所以a=2b
又椭圆过点M(4,1),所以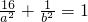 解得
解得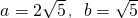
故椭圆方程为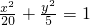
(2)将y=x+m代入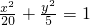
5x2+8mx+4m2-20=0
|AB|=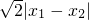 =
=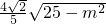 =
= ,得到m=±4
,得到m=±4
(3)设直线MA,MB的斜率分别为k1和k2,只要证明k1+k2=0
设A(x1,y1)B(x2,y2),则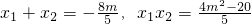
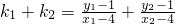 =
=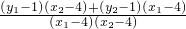
分子=(x1+m-1)(x2-4)+(x2+m-1)(x1-4)
=2x1x2+(m-5)(x1+x2)-8(m-1)
=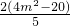
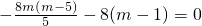
因此MA,MB与x轴所围成的三角形为等腰三角形
分析:(1)设椭圆方程为 由
由 可得a,b之间的关系,再由椭圆过点M(4,1),代入椭圆方程可得a,b得另一个关系式,联立可求
可得a,b之间的关系,再由椭圆过点M(4,1),代入椭圆方程可得a,b得另一个关系式,联立可求
(2)将y=x+m代入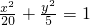 ,整理可得5x2+8mx+4m2-20=0,由|AB|=
,整理可得5x2+8mx+4m2-20=0,由|AB|=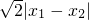 =
=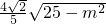 可求m
可求m
(3)设直线MA,MB的斜率分别为k1和k2,要证明直线MA,MB与x轴围成一个等腰三角形.只要证明k1+k2=0即可
点评:本题主要考查了利用椭圆的性质求解椭圆的方程,在处理直线与椭相交的位置关系的处理中,联立方程是最常用的处理方法,根与系数的关系的应用是处理此类问题的关键所在,

因为
 所以a=2b
所以a=2b又椭圆过点M(4,1),所以
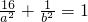 解得
解得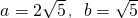
故椭圆方程为
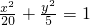
(2)将y=x+m代入
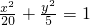
5x2+8mx+4m2-20=0
|AB|=
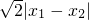 =
=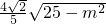 =
= ,得到m=±4
,得到m=±4(3)设直线MA,MB的斜率分别为k1和k2,只要证明k1+k2=0
设A(x1,y1)B(x2,y2),则
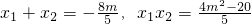
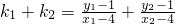 =
=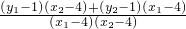
分子=(x1+m-1)(x2-4)+(x2+m-1)(x1-4)
=2x1x2+(m-5)(x1+x2)-8(m-1)
=
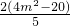
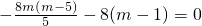
因此MA,MB与x轴所围成的三角形为等腰三角形
分析:(1)设椭圆方程为
 由
由 可得a,b之间的关系,再由椭圆过点M(4,1),代入椭圆方程可得a,b得另一个关系式,联立可求
可得a,b之间的关系,再由椭圆过点M(4,1),代入椭圆方程可得a,b得另一个关系式,联立可求(2)将y=x+m代入
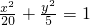 ,整理可得5x2+8mx+4m2-20=0,由|AB|=
,整理可得5x2+8mx+4m2-20=0,由|AB|=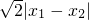 =
=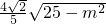 可求m
可求m(3)设直线MA,MB的斜率分别为k1和k2,要证明直线MA,MB与x轴围成一个等腰三角形.只要证明k1+k2=0即可
点评:本题主要考查了利用椭圆的性质求解椭圆的方程,在处理直线与椭相交的位置关系的处理中,联立方程是最常用的处理方法,根与系数的关系的应用是处理此类问题的关键所在,

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1.
如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1. 如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),l交椭圆于A、B两个不同点.
如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),l交椭圆于A、B两个不同点. 如图,已知椭圆的中心在原点,焦点在x轴上,离心率为
如图,已知椭圆的中心在原点,焦点在x轴上,离心率为 如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,
如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0, (2012•马鞍山二模)如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),直线l交椭圆于A、B两个不同点(A、B与M不重合).
(2012•马鞍山二模)如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),直线l交椭圆于A、B两个不同点(A、B与M不重合).