题目内容
平面α的法向量为
=(A,B,C),且经过点P(x0,y0,z0),则该平面可以用方程
| e |
A(x-x0)+B(y-y0)+C(z-z0)=0
A(x-x0)+B(y-y0)+C(z-z0)=0
来表示.分析:设出平面上的坐标Q,利用平面的法向量与平面内的向量数量积为0,求出平面的方程即可.
解答:解:设平面上的任意点的坐标Q(x,y,z),因为平面α的法向量为
=(A,B,C),且经过点P(x0,y0,z0),
所以
=(x-x0,y-y0,z-z0),
•
=0,
所以所求平面的方程为:A(x-x0)+B(y-y0)+C(z-z0)=0.
故答案为:A(x-x0)+B(y-y0)+C(z-z0)=0.
| e |
所以
| PQ |
| PQ |
| e |
所以所求平面的方程为:A(x-x0)+B(y-y0)+C(z-z0)=0.
故答案为:A(x-x0)+B(y-y0)+C(z-z0)=0.
点评:本题考查平面的法向量与平面的垂直关系,考查计算能力.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目

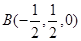 ,P(0,0,2).
,P(0,0,2).
 ,
, 于是
于是 ,所以
,所以
 设平面PCD的法向量
设平面PCD的法向量 ,
, ,即
,即 .不防设
.不防设 ,可得
,可得 .可取平面PAC的法向量
.可取平面PAC的法向量 于是
于是 从而
从而 .
. .
. ,由此得
,由此得 .
.
 ,解得
,解得 ,即
,即 .
. ,可得
,可得 ,又由
,又由 ,
, ,故
,故 .又
.又 ,所以
,所以
 于点H,连接DH.由
于点H,连接DH.由 ,可得
,可得 .
. ,从而
,从而 为二面角A-PC-D的平面角.在
为二面角A-PC-D的平面角.在 中,
中, ,由此得
,由此得 由(1)知
由(1)知 ,故在
,故在 中,
中,
 所以二面角
所以二面角 的正弦值为
的正弦值为 ,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故
,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故 或其补角为异面直线BE与CD所成的角.由于BF∥CD,故
或其补角为异面直线BE与CD所成的角.由于BF∥CD,故 .在
.在 中,
中, 故
故

 中,由
中,由 ,
, ,
,
 .由余弦定理,
.由余弦定理, ,
, 中,
中,  ,
, ,
,
 是
是 和
和 的交点, 若
的交点, 若 .
.  的长; (2)求点
的长; (2)求点 到平面
到平面 的距离;
的距离;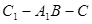 的平面角的正弦值的大小.
的平面角的正弦值的大小.
 A
A AC=3
AC=3 BC
BC ,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为
,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为
 C
C sin
sin , -
, - ) ……………………… 3分
) ……………………… 3分 =(2, -
=(2, - =(0,
-3, -h) ……… 4分
=(0,
-3, -h) ……… 4分 =(a, b, c),则可求得
=(a, b, c),则可求得 |=
|= =(x, y, z),则可求得
=(x, y, z),则可求得 满足cos
满足cos =
= ………
11分
………
11分