题目内容
(12分)在锐角三角形ABC中,∠A,∠B,∠C的对边分别为a,b,c,且b2+c2=bc+a2
(1)求∠A;
(2)若a=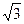 ,求b2+c2的取值范围。
,求b2+c2的取值范围。
(1)求∠A;
(2)若a=
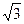 ,求b2+c2的取值范围。
,求b2+c2的取值范围。(1)
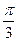
(2)5<b2+c2≤6…
①由余弦定理知:cosA=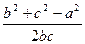 =
=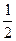
∴∠A=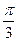 …………………………………………………5分
…………………………………………………5分
②由正弦定理得: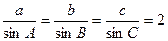
∴b=2sinB,c=2sinC
∴b2+c2=4(sin2B+sin2C)=2(1-cos2B+1-cos2C)
=4-2cos2B-2cos2(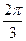 -B)
-B)
=4-2cos2B-2cos(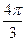 -2B)
-2B)
=4-2cos2B-2(-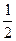 cos2B-
cos2B-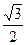 sin2B)
sin2B)
=4-cos2B+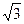 sin2B
sin2B
=4+2sin(2B-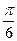 )
)
又∵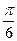 <∠B<
<∠B<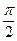
∴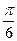 <2B-
<2B-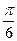 <
<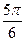
∴1<2sin(2B-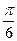 )≤2
)≤2
∴5<b2+c2≤6…………………………………………………12分
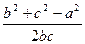 =
=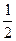
∴∠A=
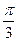 …………………………………………………5分
…………………………………………………5分②由正弦定理得:
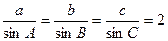
∴b=2sinB,c=2sinC
∴b2+c2=4(sin2B+sin2C)=2(1-cos2B+1-cos2C)
=4-2cos2B-2cos2(
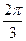 -B)
-B)=4-2cos2B-2cos(
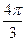 -2B)
-2B)=4-2cos2B-2(-
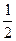 cos2B-
cos2B-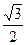 sin2B)
sin2B)=4-cos2B+
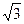 sin2B
sin2B=4+2sin(2B-
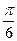 )
)又∵
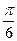 <∠B<
<∠B<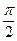
∴
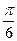 <2B-
<2B-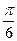 <
<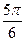
∴1<2sin(2B-
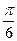 )≤2
)≤2∴5<b2+c2≤6…………………………………………………12分

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 中,
中, ,
, ,则角
,则角 等于
等于



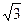 ,bc=48,b-c=2,
,bc=48,b-c=2,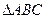 的内角A、B、C所对的边分别为
的内角A、B、C所对的边分别为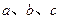 ,若
,若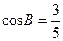
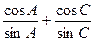 的值;
的值;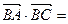 3,求
3,求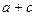 的值。
的值。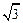 sin C.
sin C. 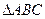 中,角
中,角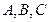 所对的边分别是
所对的边分别是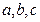 ,已知点
,已知点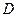 是
是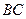 边
边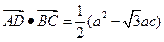 ,则角
,则角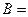 ▲ 。
▲ 。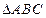 中,若
中,若 ,则
,则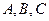 三点在曲线
三点在曲线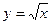 上,其横坐标依次为
上,其横坐标依次为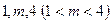 ,当
,当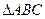 的面积最大时,
的面积最大时,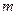 的值等于( )
的值等于( )



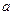 ="1, " b=
="1, " b= , ∠A=30°,则∠B等于 ( )
, ∠A=30°,则∠B等于 ( )