题目内容
已知A、B是双曲线C:
-
=1的左、右顶点,P是坐标平面上异于A、B的一点,设直线PA、PB的斜率分别为k1,k2.
求证:k1k2=
是P点在双曲线C上的充分必要条件.
| x2 |
| 4 |
| y2 |
| 3 |
求证:k1k2=
| 3 |
| 4 |
分析:从充分性、必要性两方面进行证明即可.
解答:证明:设P(x0,y0),易知A (-2,0),B (2,0)
(1)充分性:由k1k2=
知:
×
=
,
所以3x02-4y02=12,即
-
=1,
故点P在双曲线
-
=1上;
(2)必要性:因为点P在双曲线C上,
所以
-
=1,故y02=
(x02-4)
由已知x0≠±2,故k1k2=
×
=
=
综上(1)(2)知k1k2=
是P点在双曲线C上的充分必要条件.
(1)充分性:由k1k2=
| 3 |
| 4 |
| y0 |
| x0+2 |
| y0 |
| x0-2 |
| 3 |
| 4 |
所以3x02-4y02=12,即
| x02 |
| 4 |
| y02 |
| 3 |
故点P在双曲线
| x2 |
| 4 |
| y2 |
| 3 |
(2)必要性:因为点P在双曲线C上,
所以
| x02 |
| 4 |
| y02 |
| 3 |
| 3 |
| 4 |
由已知x0≠±2,故k1k2=
| y0 |
| x0+2 |
| y0 |
| x0-2 |
| y02 |
| x02-4 |
| 3 |
| 4 |
综上(1)(2)知k1k2=
| 3 |
| 4 |
点评:本题考查充要性的证明,需从充分性、必要性两方面进行证明.

练习册系列答案
相关题目
 的两个顶点,点P是双曲线上异于A,B的一点,连接PO(O为坐标原点)交椭圆
的两个顶点,点P是双曲线上异于A,B的一点,连接PO(O为坐标原点)交椭圆 于点Q,如果设直线PA,PB,QA的斜率分别为k1,k2,k3,且
于点Q,如果设直线PA,PB,QA的斜率分别为k1,k2,k3,且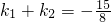 ,假设k3>0,则k3的值为
,假设k3>0,则k3的值为
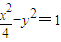 的两个顶点,点P是双曲线上异于A,B的一点,连接PO(O为坐标原点)交椭圆
的两个顶点,点P是双曲线上异于A,B的一点,连接PO(O为坐标原点)交椭圆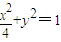 于点Q,如果设直线PA,PB,QA的斜率分别为k1,k2,k3,且
于点Q,如果设直线PA,PB,QA的斜率分别为k1,k2,k3,且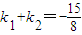 ,假设k3>0,则k3的值为( )
,假设k3>0,则k3的值为( )
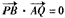 ,则双曲线C的离心率e为
,则双曲线C的离心率e为