Question

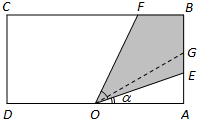如图一块长方形区域ABCD，AD=2（km），AB=1（km）．在边AD的中点O处，有一个可转动的探照灯，其照射角∠EOF始终为

π

4

，设∠AOE=α，探照灯O照射在长方形ABCD内部区域的面积为S．
（1）当0≤α＜

π

2

时，写出S关于α的函数表达式；
（2）若探照灯每9分钟旋转“一个来回”（OE自OA转到OC，再回到OA，称“一个来回”，忽略OE在OA及OC反向旋转时所用时间），且转动的角速度大小一定，设AB边上有一点G，且∠AOG=

π

6

，求点G在“一个来回”中，被照到的时间．

Answer 1

分析：（1）根据题意过点O作OH⊥BC于H．再讨论α的范围，可得当0≤α≤

π

4

时，E在边AB上，F在线段BH上，因此S=S_{正方形OABH}-S_△OAE-S_△OHF；当

π

4

＜α＜

π

2

时，E在线段BH上，F在线段CH上，因此S=S_△OEF．由此即可得到当0≤α＜

π

2

时S关于α的函数表达式；
（2）求出在“一个来回”中OE共转动的角度，并求出其中点G被照到时共转的角度，结合题意列式即可求出“一个来回”中点G被照到的时间．

解答：解：（1）过O作OH⊥BC，H为垂足．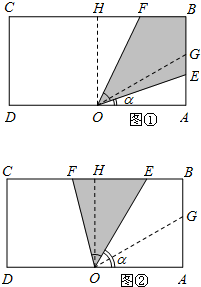
①当0≤α≤

π

4

时，E在边AB上，F在线段BH上（如图①），
此时，AE=tanα，FH=tan（

π

4

-α），
∴S=S_{正方形OABH}-S_△OAE-S_△OHF=1-

1

2

tanα-

1

2

tan（

π

4

-α）．   
②当

π

4

＜α＜

π

2

时，
E在线段BH上，F在线段CH上（如图②），
此时，EH=

1

tanα

，FH=

1

tan( 3π 4 -α)

，可得EF=

1

tanα

+

1

tan( 3π 4 -α)

．
∴S=S_△OEF=

1

2

（

1

tanα

+

1

tan( 3π 4 -α)

）．
综上所述，S=

1- 1 2 tanα- 1 2 tan( π 4 -α)   (0≤α≤ π 4 ) 1 2 ( 1 tanα + 1 tan( 3π 4 -α) )      ( π 4 ＜α＜ π 2 )

（2）在“一个来回”中，OE共转了2×

3π

4

=

3π

2

，
其中点G被照到时，共转了2×

π

6

=

π

3

 
∴在“一个来回”中，点G被照到的时间为9×

π 3

3π 2

=2（分钟）．

点评：本题以探照灯在矩形区域内照射为例，求阴影部分面积关于角α的函数关系式，并求点G在“一个来回”中，被照到的时间，着重考查了三角函数的定义、解三角形在实际问题中和函数关系式的建立等知识，属于中档题．