题目内容
已知偶函数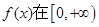 上单调递增,且
上单调递增,且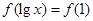 ,则x的值等于 。
,则x的值等于 。
10或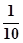
解析试题分析:因为偶函数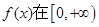 上单调递增,所以其在
上单调递增,所以其在 是减函数;又
是减函数;又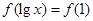 ,
,
所以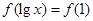 =f(-1),故lgx=1或lgx=-1,解得x=10或x=
=f(-1),故lgx=1或lgx=-1,解得x=10或x=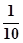 .
.
考点:本题主要考查函数的奇偶性,对数函数的性质。
点评:典型题,以常见函数为载体,综合考查函数的奇偶性、单调性等,是高考常常用到的考查方式。利用数形结合思想及转化与化归思想,问题易于得解。

练习册系列答案
相关题目
已知函数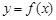 满足:①
满足:①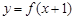 是偶函数;②在区间
是偶函数;②在区间 上是增函数.若
上是增函数.若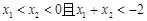 ,则
,则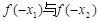 的大小关系是( )
的大小关系是( )
A.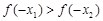 | B.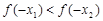 | C. | D.无法确定 |
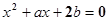 的一根在
的一根在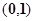 内,另一根在
内,另一根在 内,则点
内,则点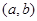 所在区域的面积为
所在区域的面积为 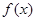 是定义域为
是定义域为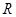 的奇函数,当
的奇函数,当 时
时 ,则当
,则当 时,
时, 
 的递减区间是 。
的递减区间是 。 ,则
,则 的值为 .
的值为 . 的定义域为
的定义域为 ,则
,则 的定义域为______ ___;
的定义域为______ ___; 的定义域是 .
的定义域是 . 为奇函数,则
为奇函数,则 .
.