题目内容
已知函数f(x)=
,画出函数f(x)的图象,求出其值域;并由f(x)=3,求x的值.
|
分析:由函数解析式可分别画出两个区间上的图象,再利用函数的单调性即可求出其值域,通过分类讨论即可求出满足f(x)=3的自变量的值.
解答:解:①如图所示,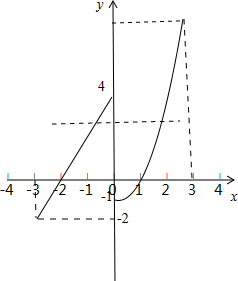
②当-3≤x<0时,∵f(x)=2x+4单调递增,因此值域为[-2,4);
当0≤x≤3时,由f(x)=x2-1单调递增,因此值域为[-1,8].
∴函数f(x)的值域为[-2,8].
③当-3≤x<0时,由f(x)=2x+4=3,解得x=-
,满足条件;
当0≤x≤3时,由f(x)=x2-1=3,解得x=2,满足条件.
综上可知:当x=-
或2时,满足f(x)=3.
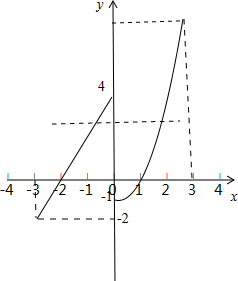
②当-3≤x<0时,∵f(x)=2x+4单调递增,因此值域为[-2,4);
当0≤x≤3时,由f(x)=x2-1单调递增,因此值域为[-1,8].
∴函数f(x)的值域为[-2,8].
③当-3≤x<0时,由f(x)=2x+4=3,解得x=-
| 1 |
| 2 |
当0≤x≤3时,由f(x)=x2-1=3,解得x=2,满足条件.
综上可知:当x=-
| 1 |
| 2 |
点评:熟练掌握一次函数和二次函数的图象和单调性是解题的关键.另外注意分类讨论的思想方法的应用.

练习册系列答案
相关题目