题目内容
已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA、QB分别切⊙M于A、B两点.(1)如果|AB|=
4
| ||
| 3 |
(2)求动弦AB的中点P的轨迹方程.
分析:(1)根据P是AB的中点,可求得|MP|,进而利用射影定理可知|MB|2=|MP|•|MQ|求得|MQ|,进而利用勾股定理在Rt△MOQ中,求得|OQ|则Q点的坐标可得,进而可求得MQ的直线方程.
(2)连接MB,MQ,设P(x,y),Q(a,0),点M、P、Q在一条直线上,利用斜率相等建立等式,进而利用射影定理|MB|2=|MP|•|MQ|,联立消去a,求得x和y的关系式,根据图形可知y<2,排除x2+(y-
)2=
.进而可求得动弦AB的中点P的轨迹方程.
(2)连接MB,MQ,设P(x,y),Q(a,0),点M、P、Q在一条直线上,利用斜率相等建立等式,进而利用射影定理|MB|2=|MP|•|MQ|,联立消去a,求得x和y的关系式,根据图形可知y<2,排除x2+(y-
| 9 |
| 4 |
| 1 |
| 16 |
解答: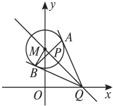 解:(1)由P是AB的中点,|AB|=
解:(1)由P是AB的中点,|AB|=
,
可得|MP|=
=
=
.
由射影定理,得|MB|2=|MP|•|MQ|,得|MQ|=3.
在Rt△MOQ中,|OQ|=
=
=
.
故Q点的坐标为(
,0)或(-
,0).
所以直线MQ的方程是2x+
y-2
=0或2x-
y+2
=0.
(2)连接MB,MQ,设P(x,y),Q(a,0),点M、P、Q在一条直线上,
得
=
.①
由射影定理,有|MB|2=|MP|•|MQ|,
即
•
=1.②
由①及②消去a,可得x2+(y-
)2=
和x2+(y-
)2=
.
又由图形可知y<2,
因此x2+(y-
)2=
舍去.
因此所求的轨迹方程为x2+(y-
)2=
(y<2).
 解:(1)由P是AB的中点,|AB|=
解:(1)由P是AB的中点,|AB|=4
| ||
| 3 |
可得|MP|=
|MA|2-(
|
1-(
|
| 1 |
| 3 |
由射影定理,得|MB|2=|MP|•|MQ|,得|MQ|=3.
在Rt△MOQ中,|OQ|=
| |MQ|2-|MO|2 |
| 32-22 |
| 5 |
故Q点的坐标为(
| 5 |
| 5 |
所以直线MQ的方程是2x+
| 5 |
| 5 |
| 5 |
| 5 |
(2)连接MB,MQ,设P(x,y),Q(a,0),点M、P、Q在一条直线上,
得
| 2 |
| -a |
| y-2 |
| x |
由射影定理,有|MB|2=|MP|•|MQ|,
即
| x2+(y-2)2 |
| a2+4 |
由①及②消去a,可得x2+(y-
| 7 |
| 4 |
| 1 |
| 16 |
| 9 |
| 4 |
| 1 |
| 16 |
又由图形可知y<2,
因此x2+(y-
| 9 |
| 4 |
| 1 |
| 16 |
因此所求的轨迹方程为x2+(y-
| 7 |
| 4 |
| 1 |
| 16 |
点评:本题主要考查了直线与圆的位置关系,求轨迹方程问题.解题过程中灵活利用了射影定理.

练习册系列答案
相关题目
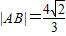 ,求直线MQ的方程;
,求直线MQ的方程;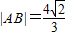 ,求直线MQ的方程;
,求直线MQ的方程;