题目内容
已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA、QB分别切⊙M于A、B两点.
(Ⅰ)求证直线AB恒过一个定点;
(Ⅱ)求动弦AB的中点P的轨迹方程.
(Ⅰ)求证直线AB恒过一个定点;
(Ⅱ)求动弦AB的中点P的轨迹方程.
分析:(Ⅰ)由题意知M,A,Q,B四点共圆,直径为MQ,由
•
=0求出圆的方程与x2+(y-2)2=1联立,消去x2+y2项得两圆公共弦AB的方程,即可证得直线AB恒过定点;
(Ⅱ)利用点M、P、Q在一条直线上,结合由射影定理,可得中点P的轨迹方程.
| MR |
| QR |
(Ⅱ)利用点M、P、Q在一条直线上,结合由射影定理,可得中点P的轨迹方程.
解答:(Ⅰ)证明:设Q(a,0),由题意知M,A,Q,B四点共圆,直径为MQ,设R(x,y)是该圆上任一点,
由
•
=0得,x(x-a)+(y-2)y=0,即x2+y2-ax-2y=0.①
①式与x2+(y-2)2=1联立,消去x2+y2项得两圆公共弦AB的方程为-ax+2y=3,
∴无论a取何值,直线AB恒过点(0,
).
(Ⅱ)解:连接MB,MQ,设P(x,y),Q(a,0),点M、P、Q在一条直线上,当a≠0时,得
=
.②
由射影定理有|MB|2=|MP|•|MQ|,即
•
=1.③
由②及③消去a,并注意到y<2,可得x2+(y-
)2=
(y<2).
当a=0时,P点为(0,
),满足方程x2+(y-
)2=
(y<2).
∴中点P的轨迹方程为x2+(y-
)2=
(y<2).
由
| MR |
| QR |
①式与x2+(y-2)2=1联立,消去x2+y2项得两圆公共弦AB的方程为-ax+2y=3,
∴无论a取何值,直线AB恒过点(0,
| 3 |
| 2 |
(Ⅱ)解:连接MB,MQ,设P(x,y),Q(a,0),点M、P、Q在一条直线上,当a≠0时,得
| 2 |
| -a |
| 2-y |
| -x |
由射影定理有|MB|2=|MP|•|MQ|,即
| x2+(y-2)2 |
| a2+4 |
由②及③消去a,并注意到y<2,可得x2+(y-
| 7 |
| 4 |
| 1 |
| 16 |
当a=0时,P点为(0,
| 3 |
| 2 |
| 7 |
| 4 |
| 1 |
| 16 |
∴中点P的轨迹方程为x2+(y-
| 7 |
| 4 |
| 1 |
| 16 |
点评:本题考查圆的方程,考查直线过定点,考查轨迹方程的求解,考查学生的计算能力,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
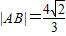 ,求直线MQ的方程;
,求直线MQ的方程;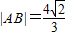 ,求直线MQ的方程;
,求直线MQ的方程;