题目内容
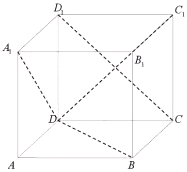
【题目】如图，
的棱长为1的正方体，任作平面
与对角线
垂直，使得与正方体的每个面都有公共点，这样得到的截面多边形的面积为
，周长为
的范围分别是_____________（用集合表示）
【答案】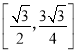
;
【解析】
由线面垂直的性质可知截面多边形的边与所在的正方形的对角线平行，利用相似比即可求得截面周长为定值.
连接
，
，
，
，
平面
，又
平面
，
同理可证
则
平面
，
设平面
与平面的交线为
，
则
，又
，
，
同理可得平面与其他各面的交线都与此平面的对角线平行，
设
，则
，
，
，
同理可得六边形其他相邻两边的和为
,
六边形的周长
为定值
.
因为截面与各面的交线与各面的对角线平行，所以不管六边形如何变化，六边形的每个内角都是
，并且相邻边长的和为，通过构造边长为的菱形，并且有一个角为
，
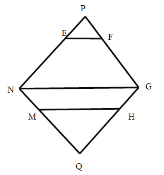
六边形
的面积是如图两个等边三角形的面积减上下两个等边三角形的面积，
，
，
，
，
所以截面多边形面积的取值范围是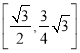
故答案为：；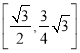
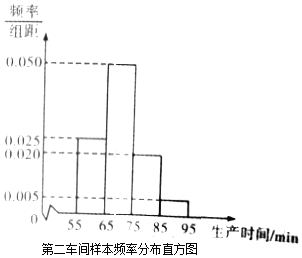
【题目】某工厂有两个车间生产同一种产品，第一车间有工人200人，第二车间有工人400人，为比较两个车间工人的生产效率，采用分层抽样的方法抽取工人，并对他们中每位工人生产完成一件产品的时间（单位：min）分别进行统计，得到下列统计图表（按照[55，65），[65，75），[75，85），[85，95]分组）．
分组 | 频数 |
[55，65） | 2 |
[65，75） | 4 |
[75，85） | 10 |
[85，95] | 4 |
合计 | 20 |
第一车间样本频数分布表
（Ⅰ）分别估计两个车间工人中，生产一件产品时间小于75min的人数；
（Ⅱ）分别估计两车间工人生产时间的平均值，并推测哪个车间工人的生产效率更高？（同一组中的数据以这组数据所在区间中点的值作代表）
（Ⅲ）从第一车间被统计的生产时间小于75min的工人中，随机抽取3人，记抽取的生产时间小于65min的工人人数为随机变量X，求X的分布列及数学期望．
