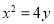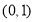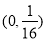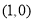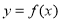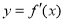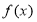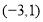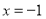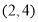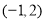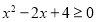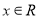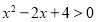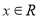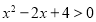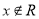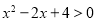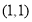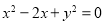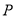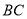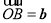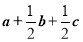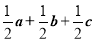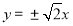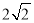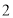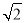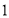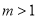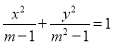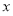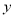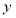题目内容
在平面直角坐标系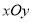 中,已知点
中,已知点 ,动点
,动点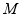 在
在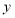 轴上的正射影为点
轴上的正射影为点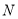 ,且满足直线
,且满足直线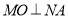 .
.
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)当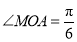 时,求直线
时,求直线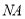 的方程.
的方程.
(Ⅰ)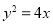 (
(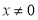 );(Ⅱ)
);(Ⅱ)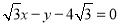 或
或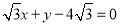
【解析】
试题分析:(Ⅰ)属直接法求轨迹问题,再根据 列式子时,可根据直线垂直斜率相乘等于
列式子时,可根据直线垂直斜率相乘等于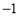 列出方程,但需注意斜率存在与否的问题,还可转化为向量垂直问题,用数量积为0列出方程(因此法不用讨论故常选此法解决直线垂直问题)。因点
列出方程,但需注意斜率存在与否的问题,还可转化为向量垂直问题,用数量积为0列出方程(因此法不用讨论故常选此法解决直线垂直问题)。因点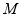 不能与原点重合故
不能与原点重合故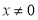 。(Ⅱ)
。(Ⅱ) 即直线
即直线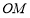 的倾斜角为
的倾斜角为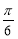 或
或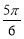 。故可求出直线
。故可求出直线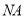 的斜率,由点斜式可求直线
的斜率,由点斜式可求直线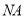 的方程。
的方程。
试题解析:【解析】
(Ⅰ)设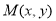 ,则
,则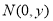 ,
,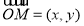 ,
, . 2分
. 2分
因为 直线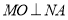 ,
,
所以 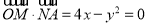 ,即
,即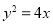 . 4分
. 4分
所以 动点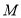 的轨迹C的方程为
的轨迹C的方程为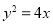 (
(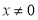 ). 5分
). 5分
(Ⅱ)当 时,因为
时,因为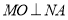 ,所以
,所以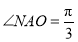 .
.
所以 直线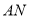 的倾斜角为
的倾斜角为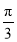 或
或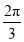 .
.
当直线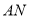 的倾斜角为
的倾斜角为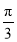 时,直线
时,直线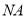 的方程为
的方程为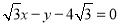 ; 8分
; 8分
当直线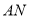 的倾斜角为
的倾斜角为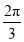 时,直线
时,直线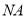 的方程为
的方程为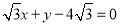 . 10分
. 10分
考点:1、求轨迹方程;2、直线方程的点斜式。

练习册系列答案
相关题目