题目内容
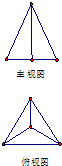 (2012•吉安二模)如右图是底面积为
(2012•吉安二模)如右图是底面积为| 3 |
| 3 |
分析:先求出下底面的边长,得到侧视图的一条边长,再根据三棱锥的高就是侧视图的高,利用体积公式求出高,代入三角形的面积公式得到结果.
解答:解:由题知几何体是一个正三棱锥,
因为底面积为
=
•a•a•sin60°⇒a=2;
即三棱锥的底面是一个边长为2的正三角形,
∴侧视图的一条边长是下底面三角形的高为:
×2=
,
又因为三棱锥的高就是侧视图的高,高是
=
=3,
∴侧视图的面积是
×
×3=
.
故选:B.
因为底面积为
| 3 |
| 1 |
| 2 |
即三棱锥的底面是一个边长为2的正三角形,
∴侧视图的一条边长是下底面三角形的高为:
| ||
| 2 |
| 3 |
又因为三棱锥的高就是侧视图的高,高是
| V | ||
|
| ||||
|
∴侧视图的面积是
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
故选:B.
点评:本题考查由三视图还原几何体并且看出几何体各个部分的长度,本题解题的关键是求出几何体的侧视图中的边长.

练习册系列答案
相关题目
