题目内容
在 中,若边长和内角满足
中,若边长和内角满足 ,则角
,则角 的值是( )
的值是( )
A. | B. 或 或 | C. | D. 或 或 |
C
解析试题分析:在 中,由正弦定理得:
中,由正弦定理得: 即
即 ,有因为
,有因为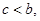 所以角
所以角 为锐角,所以
为锐角,所以
考点:本小题主要考查三角形中正弦定理的应用和解的情况的判断.
点评:利用正弦定理解三角形时,一般利用大边对大角来判断三角形解的个数.

练习册系列答案
相关题目
 的内角
的内角 的对边分别为
的对边分别为 ,若
,若
 ,则
,则 等于( )
等于( )
A. | B.2 | C. | D.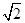 |
 ,若
,若 ,则
,则 的形状为( )
的形状为( )
| A.等腰三角形 | B.等腰直角三角形 | C.直角三角形 | D.等边三角形 |
在 中,已知
中,已知 ,
, ,
, ,P为线段AB上
,P为线段AB上
的一点,且 .
. ,则
,则 的最小值为( )
的最小值为( )
A. | B. | C. | D.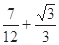 |
已知 中,
中, .则
.则 ( )。
( )。
A. | B. | C. 或 或 | D. 或 或 |
已知 满足
满足 ,则
,则 的形状是( )
的形状是( )
| A.等腰三角形 | B.直角三角形 |
| C.等腰直角三角形 | D.等腰三角形或直角三角形 |
在 ABC中,B=60o,
ABC中,B=60o, ,则这个三角形是( )
,则这个三角形是( )
| A.不等边三角形 | B.等边三角形 | C.等腰三角形 | D.直角三角形 |
设 为△
为△ 的重心,且
的重心,且 ,则
,则 的大小为
的大小为
| A.450 | B.600 | C.300 | D.150 |
 中,
中, ,则A等于 ( )
,则A等于 ( )