题目内容
已知 满足
满足 ,则
,则 的形状是( )
的形状是( )
| A.等腰三角形 | B.直角三角形 |
| C.等腰直角三角形 | D.等腰三角形或直角三角形 |
A
解析试题分析:因为对于三角形形状的判定要不就通过角,要不就通过边,那么可以利用正弦定理进行边角转化,由 ,
,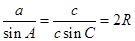 得到sinC2R=2sinA2RcosB.化简得到为sinC=2cosBsinA=sin(B+A)=sinBcosA+cosBsinA,这样可得到sin(B-A)=0,故有A=B因此该三角形为等腰三角形,选A
得到sinC2R=2sinA2RcosB.化简得到为sinC=2cosBsinA=sin(B+A)=sinBcosA+cosBsinA,这样可得到sin(B-A)=0,故有A=B因此该三角形为等腰三角形,选A
考点:本试题主要考查了正弦定理、两角和差的三角公式和三角形的内角和定理的综合运用,
点评:解决该试题的关键是对于边化角后,能运用内角和定理中sinA=sin(C+B),化简变形得到结论。

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
若DABC中,sinA:sinB:sinC = 2:3:4,那么cosC =( )
A. | B. | C. | D. |
已知 是
是 的一个内角,若
的一个内角,若 ,则
,则 是( )
是( )
| A.钝角三角形 | B.锐角三角形 |
| C.直角三角形 | D.任意三角形 |
在 中,若边长和内角满足
中,若边长和内角满足 ,则角
,则角 的值是( )
的值是( )
A. | B. 或 或 | C. | D. 或 或 |
下列已知△ABC的两边及其中一边对角的条件中,正确的是( )
A. 有两解 有两解 | B. 有一解 有一解 |
C. 无解 无解 | D. 有一解 有一解 |
边长为5,7,8的三角形中,最大角与最小角之和为 ( )
A. | B. | C. | D. |
在△ 中,若
中,若 ,则
,则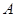 等于( )
等于( )
A. | B. | C. | D. |
在 中,若
中,若 ,则
,则 的形状一定是( )
的形状一定是( )
| A.锐角三角形 | B.钝角三角形 |
| C.直角三角形 | D.等腰三角形 |
 中,若
中,若 ,则
,则 等于 ( )
等于 ( ) B
B  C
C  D
D 