题目内容
如图2-3-10,在△OAB中,若OA =OB =2a,⊙O的半径r =a.问:AB与⊙O相切、相交、相离时,∠AOB的取值范围如何?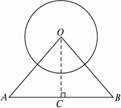
图2-3-10
思路分析:先作出O到AB的距离OC,根据AB与⊙O的不同位置关系确定OC的取值范围,从而再确定∠AOB的取值范围.
解:过O作OC⊥AB,垂足为C,?
(1)当AB与⊙O相切时,OC =r =a,此时cos∠AOC =![]() =
=![]() ,?
,?
∴∠AOC=60°.?
又∵OA =OB,∴OC平分∠AOB.?
∴∠AOB =120°.?

(2)当AB与⊙O相交时,OC <r =a,此时cos∠AOC <![]() ,?
,?
∴60°<∠AOC<90°.?
∴120°<∠AOB<180°.?
(3)当AB与⊙O相离时,OC >r,此时cos∠AOC >![]() ,?
,?
∴0°<∠AOC <60°.∴0°<∠AOB<120°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
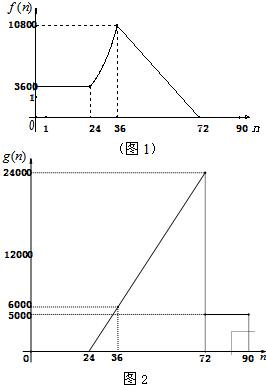 2010年上海世博会组委会为保证游客参观的顺利进行,对每天在各时间段进入园区和离开园区的人数作了一个模拟预测.为了方便起见,以10分钟为一个计算单位,上午9点10分作为第一个计算人数的时间,即n=1;9点20分作为第二个计算人数的时间,即n=2;依此类推…,把一天内从上午9点到晚上24点分成了90个计算单位.
2010年上海世博会组委会为保证游客参观的顺利进行,对每天在各时间段进入园区和离开园区的人数作了一个模拟预测.为了方便起见,以10分钟为一个计算单位,上午9点10分作为第一个计算人数的时间,即n=1;9点20分作为第二个计算人数的时间,即n=2;依此类推…,把一天内从上午9点到晚上24点分成了90个计算单位.