题目内容
将函数y=Asin2x的图象按向量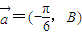
平移，得到函数y=f（x）的图象．若函数f（x）在点
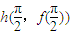处的切线恰好经过坐标原点，则下列结论正确的是（ ）A．
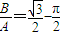
B．
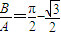
C．
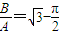
D．
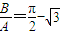
【答案】分析：求出函数平移后的解析式，通过函数的导数，求出切线的斜率，利用切线经过原点，求出A，B关系，得到选项．
解答：解：函数y=Asin2x的图象按向量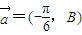
平移，得到函数y=f（x）的图象．
所以函数f（x）=Asin（2x+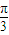
）+B，所以f′（x）=2Acos（2x+
），
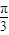函数f（x）在点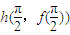
处，即
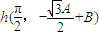处的切线的斜率为k=-A．
切线恰好经过坐标原点，所以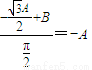
，
即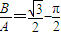
．
故选A．
点评：本题是中档题，考查函数图象的平移变换，函数的导数与切线的斜率的关系，考查计算能力．
解答：解：函数y=Asin2x的图象按向量
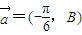平移，得到函数y=f（x）的图象．所以函数f（x）=Asin（2x+
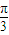）+B，所以f′（x）=2Acos（2x+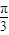），函数f（x）在点
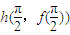处，即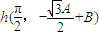处的切线的斜率为k=-A．切线恰好经过坐标原点，所以
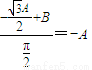，即
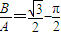．故选A．
点评：本题是中档题，考查函数图象的平移变换，函数的导数与切线的斜率的关系，考查计算能力．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目