题目内容
方程|x-| 4-y2 |
| 4-x2 |
分析:曲线方程即 x2+y2=4,且 x≥0,y≤0,表示以原点为圆心,以2为半径的圆位于第四象限内的部分,
包括与轴的交点,如图所示,从而求得直线y=x+b 在y轴上的截距b的取值范围.
包括与轴的交点,如图所示,从而求得直线y=x+b 在y轴上的截距b的取值范围.
解答: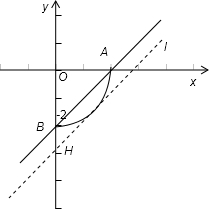 解:∵由 方程|x-
解:∵由 方程|x-
|+|y+
|=0,
可得 |x-
| =0 且 |y+
|=0,
∴x2+y2=4且x≥0,y≤0,表示以原点为圆心,以2为半径的圆位于第四象限内的部分,
包括与轴的交点,如图所示:
当直线与AB重合时,曲线与直线有两个交点,
当直线与l重合时,曲线与直线相切,仅有一个交点,
AB在y轴上的截距为-2,易知直线l在y轴上的截距为-2
,且AB∥直线l,故实数b的取值范围是[-2
,-2],
故答案为 [-2
,-2].
 解:∵由 方程|x-
解:∵由 方程|x-| 4-y2 |
| 4-x2 |
可得 |x-
| 4-y2 |
| 4-x2 |
∴x2+y2=4且x≥0,y≤0,表示以原点为圆心,以2为半径的圆位于第四象限内的部分,
包括与轴的交点,如图所示:
当直线与AB重合时,曲线与直线有两个交点,
当直线与l重合时,曲线与直线相切,仅有一个交点,
AB在y轴上的截距为-2,易知直线l在y轴上的截距为-2
| 2 |
| 2 |
故答案为 [-2
| 2 |
点评:本题考查直线和圆锥曲线的位置关系,得到 x2+y2=4,且 x≥0,y≤0,并画出图象是解题的关键.

练习册系列答案
相关题目