题目内容
已知函数y=|cosx+sinx|.(1)画出函数在x∈[-
| π |
| 4 |
| 7π |
| 4 |
(2)写出函数的最小正周期和单调递增区间;试问:当x为何值时,函数有最大值?最大值是多少?
(3)若x是△ABC的一个内角,且y2=1,试判断△ABC的形状.
分析:(1)化简函数y=|cosx+sinx|为
|sin(x+
)|,然后画出函数在x∈[-
,
]的简图;
(2)直接求出函数的最小正周期和单调递增区间;结合图象容易推出,函数的最大值,以及x的值.
(3)x是△ABC的一个内角,且y2=1,求出x的值,从而判断△ABC的形状.
| 2 |
| π |
| 4 |
| π |
| 4 |
| 7π |
| 4 |
(2)直接求出函数的最小正周期和单调递增区间;结合图象容易推出,函数的最大值,以及x的值.
(3)x是△ABC的一个内角,且y2=1,求出x的值,从而判断△ABC的形状.
解答: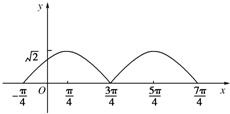 解:(1)∵y=|cosx+sinx|=
解:(1)∵y=|cosx+sinx|=
|sin(x+
)|,当x∈[-
,
]时,其图象如图所示.
(2)函数的最小正周期是π,其单调递增区间是[kπ-
,kπ+
](k∈Z).
由图象可以看出,当x=kπ+
(k∈Z)时,该函数的最大值是
.
(3)若x是△ABC的一个内角,则有0<x<π,
∴0<2x<2π.由y2=1,
得|cosx+sinx|2=1?1+sin2x=1.
∴sin2x=0,∴2x=π,x=
,
故△ABC为直角三角形.
 解:(1)∵y=|cosx+sinx|=
解:(1)∵y=|cosx+sinx|=| 2 |
| π |
| 4 |
| π |
| 4 |
| 7π |
| 4 |
(2)函数的最小正周期是π,其单调递增区间是[kπ-
| π |
| 4 |
| π |
| 4 |
由图象可以看出,当x=kπ+
| π |
| 4 |
| 2 |
(3)若x是△ABC的一个内角,则有0<x<π,
∴0<2x<2π.由y2=1,
得|cosx+sinx|2=1?1+sin2x=1.
∴sin2x=0,∴2x=π,x=
| π |
| 2 |
故△ABC为直角三角形.
点评:本题考查余弦函数的图象,三角函数的周期性及其求法,正弦函数的图象,三角函数的最值,考查作图能力,计算能力,是中档题.

练习册系列答案
相关题目
 已知函数y=cos(ωx+?)(ω>0,?∈(-π,π))的部分图象如右图所示,则?的值为( )
已知函数y=cos(ωx+?)(ω>0,?∈(-π,π))的部分图象如右图所示,则?的值为( ) (2013•无为县模拟)已知函数y=cos(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示,则( )
(2013•无为县模拟)已知函数y=cos(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示,则( )